题目内容
12.已知等比数列{an}的前n项和为Sn,若S3=3a1,且a4=8,则S10=341或80.分析 由已知数据可得首项和公比的方程组,解方程组代入求和公式可得.
解答 解:设等比数列{an}的公比为q,
∵S3=3a1,且a4=8,
∴a1(1+q+q2)=3a1,a4=a1q3=8,
联立解得q=-2且a1=-1或q=1且a1=8;
当q=-2且a1=-1时,S10=$\frac{-1(1-{2}^{10})}{1-(-2)}$=341;
当q=1且a1=8时,S10=10a1=80
故答案为:341或80
点评 本题考查等比数列的通项公式和求和公式,属基础题.

练习册系列答案
相关题目
3.已知点A,B,C,P在同一平面内,且$\overrightarrow{PQ}$=$\frac{1}{3}$$\overrightarrow{PA}$,$\overrightarrow{QR}$=$\frac{1}{3}$$\overrightarrow{QB}$,$\overrightarrow{RP}$=$\frac{1}{3}$$\overrightarrow{RC}$,则△ABC与△PBC的面积之比是( )
| A. | 14:3 | B. | 19:4 | C. | 24:5 | D. | 29:6 |
7.化简:$\frac{1-co{s}^{4}α-si{n}^{4}α}{1-co{s}^{6}α-si{n}^{6}α}$的值为( )
| A. | $\frac{2}{3}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
17.复数z=|$\sqrt{3}$-i|+i(i为虚数单位),则复数z的共轭复数为( )
| A. | 2-i | B. | 2+i | C. | 4-i | D. | 4+i |
2.在北方某城市随机选取一年内40天的空气污染指数(API)的监测数据,统计结果如下:
(Ⅰ)已知污染指数API大于250为重度污染,若本次抽取样本数据有9天是在供暖季,其中有3天为重度污染,完成下面的2×2列联表,问有多大把握认为该城市空气重度污染与供暖有关?
(Ⅱ)在样本中,从污染指数API大于250的6天中任取2天,求至少有1天API大于300的概率.
附注:k2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d
| API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | (300,+∞) |
| 天数 | 3 | 5 | 8 | 10 | 8 | 4 | 2 |
| 非重度污染 | 重度污染 | 合计 | |
| 供暖季 | |||
| 非供暖季 | |||
| 合计 | 40 |
附注:k2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.025 | 6.635 | 7.879 | 10.828 |
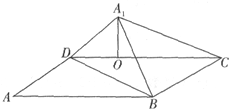 如图,将矩形ABCD沿对角线BD把△ABD折起,使A点移到A1点,且A1在平面BCD上的射影O恰好在CD上.
如图,将矩形ABCD沿对角线BD把△ABD折起,使A点移到A1点,且A1在平面BCD上的射影O恰好在CD上.