题目内容
11．根据数列的前几项，写出一个通项公式：（1）-1，7，-13，19，…；
（2）0.8，0.88，0.888，…；
（3）-$\frac{1}{2}$，$\frac{1}{4}$，-$\frac{5}{8}$，$\frac{13}{16}$，-$\frac{29}{32}$，$\frac{61}{64}$…；
（4）$\frac{3}{2}$，1，$\frac{7}{10}$，$\frac{9}{17}$，…；
（5）0，1，0，1，…．
分析 观察数列的前几项的形式，从而写出通项公式．
解答 解：（1）an=（-1）n（6n-5）；
（2）an=$\frac{8}{9}$（1-$\frac{1}{1{0}^{n}}$）；
（3）an=$\left\{\begin{array}{l}{-\frac{1}{2}，n=1}\\{（-1）^{n}\frac{{2}^{n}-3}{{2}^{n}}，n≥2}\end{array}\right.$；
（4）an=$\frac{2n+1}{{n}^{2}+1}$；
（5）an=$\frac{（-1）^{n}+1}{2}$．
点评 本题考查了数列的应用，属于基础题．
练习册系列答案
相关题目
6．已知直线y=kx与函数f（x）=$\left\{\begin{array}{l}{2-（\frac{1}{2}）^{x}，x≤0}\\{\frac{1}{2}{x}^{2}-x+1，x＞0}\end{array}\right.$的图象恰好有3个不同的公共点，则实数k的取值范围是（ ）
| A． | （$\sqrt{2}$-1，+∞） | B． | （0，$\sqrt{2}$-1） | C． | （-$\sqrt{2}$-1，$\sqrt{2}$-1） | D． | （-∞，-$\sqrt{2}$-1）∪（$\sqrt{2}$-1，+∞） |
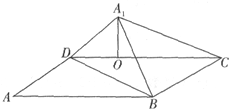如图，将矩形ABCD沿对角线BD把△ABD折起，使A点移到A1点，且A1在平面BCD上的射影O恰好在CD上．