题目内容
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() 为常数,
为常数,![]() 是自然对数的底数.
是自然对数的底数.
(1)设![]() ,若函数
,若函数![]() 在区间
在区间![]() 上有极值点,求实数
上有极值点,求实数![]() 的取值范围;
的取值范围;
(2)证明:当![]() 时,
时,![]() 恒成立.
恒成立.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)![]() ,则
,则![]() ,若
,若![]() 在
在![]() 上有极值点,则
上有极值点,则![]() 在
在![]() 上有变号零点,设
上有变号零点,设![]() 研究单调性使得函数和x轴有两个交点即可;(2)要证
研究单调性使得函数和x轴有两个交点即可;(2)要证![]() 成立,
成立,![]() ,
,![]()
分别求得左式的最大值和右式的最小值,证得最大值小于最小值即可.
解析:
(1)由题意,![]() ,则
,则![]() ,
,
由题意,若![]() 在
在![]() 上有极值点,
上有极值点,
则![]() 在
在![]() 上有变号零点.
上有变号零点.
令![]() ,即
,即![]() ,
,
设![]() ,
,![]() ,
,
故![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,
即![]() .
.
故若函数![]() 在
在![]() 上有极值点,
上有极值点,
只需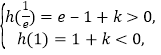
则![]() ,
,
所以![]() 的取值范围为
的取值范围为![]() .
.
(2)由题意,知要证![]() 成立.
成立.
设![]() ,
,![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
所以当![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
所以![]() .
.
设![]() ,
,![]() ,
,
则![]() ,
,
因为![]() ,则
,则![]() ,
,
故![]() 在区间
在区间![]() 内单调递增,
内单调递增,
故![]() ,即
,即![]() .
.
所以![]() ,
,
故![]() .
.
综上,当![]() 时,
时,![]() .
.
命题得证.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案【题目】市场份额又称市场占有率,它在很大程度上反映了企业的竞争地位和盈利能力,是企业非常重视的一个指标.近年来,服务机器人与工业机器人以迅猛的增速占领了中国机器人领域庞大的市场份额,随着“一带一路”的积极推动,包括机器人产业在内的众多行业得到了更广阔的的发展空间,某市场研究人员为了了解某机器人制造企业的经营状况,对该机器人制造企业2017年1月至6月的市场份额进行了调查,得到如下资料:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
市场份额 | 11 | 163 | 16 | 15 | 20 | 21 |
请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程,并预测该企业2017年7月份的市场份额.
的线性回归方程,并预测该企业2017年7月份的市场份额.
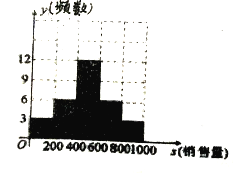
如图是该机器人制造企业记录的2017年6月1日至6月30日之间的产品销售频数(单位:天)统计图.设销售产品数量为![]() ,经统计,当
,经统计,当![]() 时,企业每天亏损约为200万元;
时,企业每天亏损约为200万元;
当![]() 时,企业平均每天收入约为400万元;
时,企业平均每天收入约为400万元;
当![]() 时,企业平均每天收入约为700万元.
时,企业平均每天收入约为700万元.
①设该企业在六月份每天收入为![]() ,求
,求![]() 的数学期望;
的数学期望;
②如果将频率视为概率,求该企业在未来连续三天总收入不低于1200万元的概率.
附:回归直线的方程是![]() ,其中
,其中
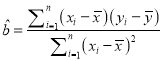 ,
, ![]() ,
,
![]()