题目内容
已知数列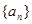 的各项均为正数,
的各项均为正数,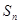 表示该数列前
表示该数列前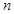 项的和,且满足
项的和,且满足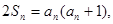
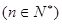 ,设
,设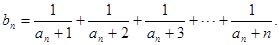
(1)求数列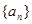 的通项; (2)证明:数列
的通项; (2)证明:数列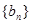 为递增数列;
为递增数列;
(3)是否存在正整数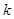 ,使得
,使得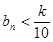 对任意正整数
对任意正整数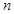 恒成立,若存在,求出
恒成立,若存在,求出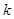 的最小值。
的最小值。
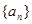 的各项均为正数,
的各项均为正数,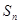 表示该数列前
表示该数列前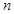 项的和,且满足
项的和,且满足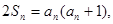
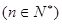 ,设
,设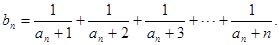
(1)求数列
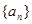 的通项; (2)证明:数列
的通项; (2)证明:数列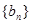 为递增数列;
为递增数列;(3)是否存在正整数
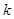 ,使得
,使得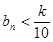 对任意正整数
对任意正整数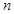 恒成立,若存在,求出
恒成立,若存在,求出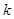 的最小值。
的最小值。(1)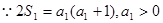 ,得:
,得: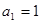 (2分);
(2分);
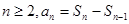 ,
,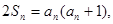
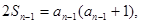 得:
得:
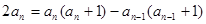
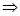
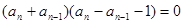 ,
,
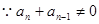 ,
,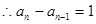 ,
,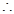 数列
数列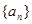 为等差数列,故
为等差数列,故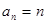 ……… 3分;
……… 3分;
(2)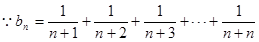
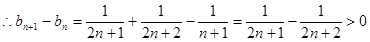
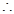 数列
数列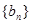 为递增数列; ……… 6分
为递增数列; ……… 6分
(3)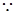
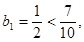
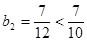 ,
,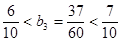
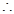 若存在,必有
若存在,必有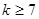 ,………8分
,………8分
又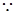 当
当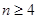 时,
时,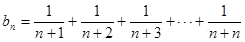
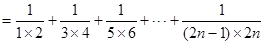
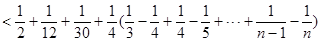
=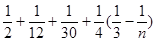
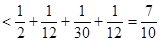 ………10分
………10分
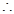 这样正整数
这样正整数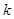 存在,
存在,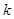 的最小值为7.
的最小值为7.
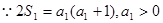 ,得:
,得: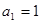 (2分);
(2分);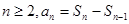 ,
,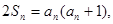
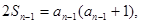 得:
得: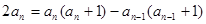
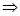
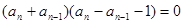 ,
,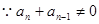 ,
,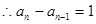 ,
,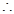 数列
数列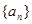 为等差数列,故
为等差数列,故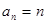 ……… 3分;
……… 3分;(2)
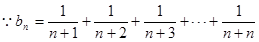
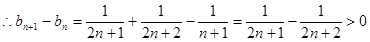
 数列
数列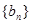 为递增数列; ……… 6分
为递增数列; ……… 6分(3)
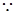
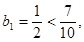
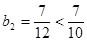 ,
,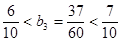
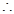 若存在,必有
若存在,必有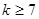 ,………8分
,………8分又
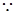 当
当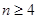 时,
时,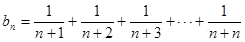
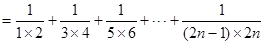
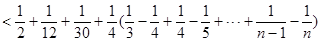
=
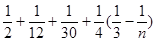
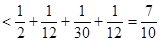 ………10分
………10分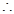 这样正整数
这样正整数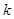 存在,
存在,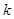 的最小值为7.
的最小值为7.略

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
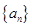 为等差数列,则下列数列中,成等差数列的个数为( )
为等差数列,则下列数列中,成等差数列的个数为( )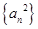 ②
② ③
③ ④
④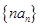 (p、q为非零常数)
(p、q为非零常数)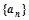 是公比大于1的等比数列,Sn为数列
是公比大于1的等比数列,Sn为数列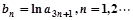 ,求数列
,求数列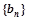 的前n项和Tn.
的前n项和Tn.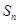 是等差数列
是等差数列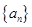 的前
的前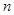 项和,若
项和,若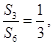 则
则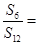
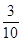
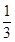
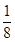
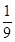
 的前
的前 项和为
项和为 则
则 ( )
( )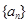 的公差
的公差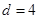 ,且
,且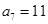 ,若
,若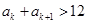 ,则正整数
,则正整数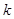 的最小值为 .
的最小值为 .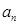 }是公差不为0的等差数列,{
}是公差不为0的等差数列,{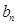 } 是等比数列,其中
} 是等比数列,其中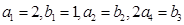 ,且存在常数α、β ,使得
,且存在常数α、β ,使得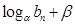 对每一个正整数
对每一个正整数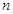 都成立,则
都成立,则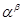 = .
= .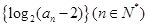 为等差数列,且
为等差数列,且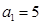 ,
,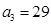 .
.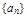 的通项公式;
的通项公式; 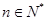 ,
,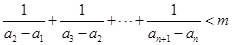 恒成立的实数m是否存在最小值?如果存在,求出m的最小值;
恒成立的实数m是否存在最小值?如果存在,求出m的最小值; 如果不存在,说明理由.
如果不存在,说明理由.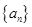 为等差数列,
为等差数列,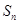 为其前
为其前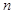 项和,且
项和,且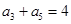 ,则
,则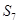 等于( )
等于( )