题目内容
已知{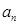
}是公差不为0的等差数列,{
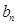} 是等比数列,其中
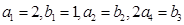,且存在常数α、β ,使得=
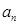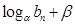对每一个正整数
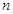都成立,则
= ．
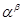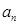}是公差不为0的等差数列,{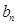} 是等比数列,其中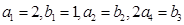,且存在常数α、β ,使得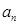=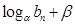对每一个正整数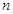都成立,则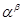= ．4
略
练习册系列答案
字词句段篇系列答案
相关题目
字词句段篇系列答案题目内容
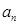}是公差不为0的等差数列,{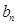} 是等比数列,其中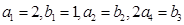,且存在常数α、β ,使得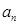=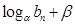对每一个正整数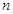都成立,则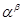= ．字词句段篇系列答案
中，首项
，数列
满足
．
满足
，
.
满足
，求数列
的各项均为正数，
表示该数列前
项的和，且满足
，设
为递增数列；
，使得
对任意正整数
中，
，记
，则
的值为（ ）
的前
项和为
，且
．
，
中的部分项
恰好组成等比数列，且
，求该等比数列的公比与数列
的通项公式。
是等差数列
的前n项和，已知
，
，则
等于( ) 
中，
，
，则
项和
__________
，如果存在实常数
，使得
对于任意
都成立，我们称数列
类数列”．
是 “
，求它对应的实常数
满足
，
，求数列