题目内容
设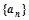 是公比大于1的等比数列,Sn为数列
是公比大于1的等比数列,Sn为数列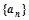 的前n项和.已知S3=7,且a1+3,3a2,a3+4构成等差数列.
的前n项和.已知S3=7,且a1+3,3a2,a3+4构成等差数列.
(1)求数列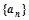 的通项公式;
的通项公式;
(2)令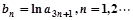 ,求数列
,求数列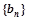 的前n项和Tn.
的前n项和Tn.
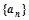 是公比大于1的等比数列,Sn为数列
是公比大于1的等比数列,Sn为数列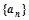 的前n项和.已知S3=7,且a1+3,3a2,a3+4构成等差数列.
的前n项和.已知S3=7,且a1+3,3a2,a3+4构成等差数列.(1)求数列
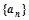 的通项公式;
的通项公式;(2)令
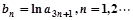 ,求数列
,求数列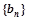 的前n项和Tn.
的前n项和Tn.(Ⅰ)设数列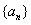 的公比为
的公比为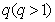 ,
,
由已知,得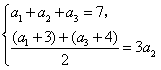 , ……………………………………2分
, ……………………………………2分
即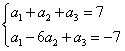 , 也即
, 也即 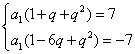
解得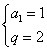 ……………………………………………………5分
……………………………………………………5分
故数列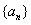 的通项为
的通项为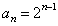 . ……………………………………6分
. ……………………………………6分
(Ⅱ)由(Ⅰ)得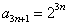 , ∴
, ∴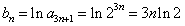 ,……8分
,……8分
又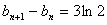 ,
,
∴ 是以
是以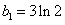 为首项,以
为首项,以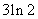 为公差的等差数列 ………10分
为公差的等差数列 ………10分
∴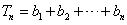
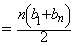
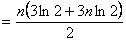
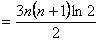
即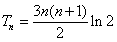 .
.
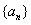 的公比为
的公比为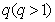 ,
,由已知,得
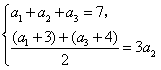 , ……………………………………2分
, ……………………………………2分即
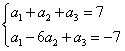 , 也即
, 也即 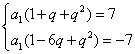
解得
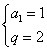 ……………………………………………………5分
……………………………………………………5分故数列
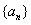 的通项为
的通项为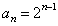 . ……………………………………6分
. ……………………………………6分(Ⅱ)由(Ⅰ)得
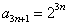 , ∴
, ∴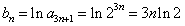 ,……8分
,……8分又
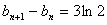 ,
,∴
 是以
是以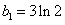 为首项,以
为首项,以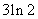 为公差的等差数列 ………10分
为公差的等差数列 ………10分∴
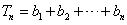
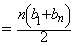
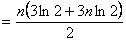
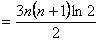
即
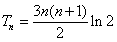 .
.分析:(1)由{an}是公比大于1的等比数列,S
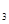 =7,且a
=7,且a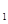 +3,3a
+3,3a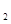 ,a
,a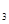 +4构成等差数列,我们不难构造方程组,解方程组即可求出相关基本量,进而给出数列{an}的通项公式.
+4构成等差数列,我们不难构造方程组,解方程组即可求出相关基本量,进而给出数列{an}的通项公式.(2)由b
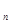 =lna
=lna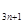 ,n=1,2,…,我们易给出数列{b
,n=1,2,…,我们易给出数列{b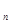 }的通项公式,分析后可得:数列{b
}的通项公式,分析后可得:数列{b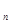 }是一个等差数列,代入等差数列前n项和公式即可求出T
}是一个等差数列,代入等差数列前n项和公式即可求出T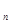
解答:解:(1)由已知得:
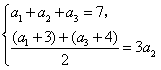
解得a
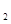 =2.
=2.设数列{a
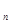 }的公比为q,由a
}的公比为q,由a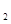 =2,
=2,可得a
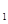 =
=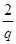 ,a
,a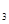 =2q.
=2q.又S
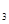 =7,可知
=7,可知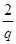 +2+2q=7,
+2+2q=7,即2q
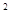 -5q+2=0,
-5q+2=0,解得q
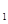 =2,q
=2,q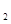 =
=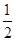
由题意得q>1,
∴q=2
∴a
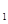 =1.故数列{an}的通项为a
=1.故数列{an}的通项为a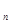 =2
=2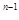 .
.(2)由于b
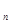 =lna
=lna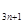 ,n=1,2,
,n=1,2,由(1)得a
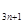 =2
=2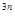
∴b
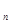 =ln2
=ln2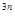 =3nln2又b
=3nln2又b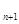 -b
-b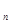 =3ln2
=3ln2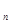
∴{b
 }是等差数列.
}是等差数列.∴T
 =b
=b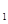 +b
+b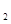 ++b
++b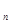
=
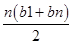
=
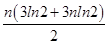
=
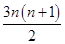 ln2.
ln2.故T
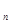 =
=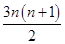 ln2.
ln2.点评:解答特殊数列(等差数列与等比数列)的问题时,根据已知条件构造关于基本量的方程,解方程求出基本量,再根据定义确定数列的通项公式及前n项和公式,然后代入进行运算.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
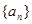 的各项均为正数,
的各项均为正数,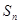 表示该数列前
表示该数列前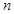 项的和,且满足
项的和,且满足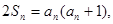
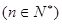 ,设
,设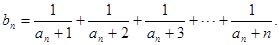
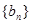 为递增数列;
为递增数列;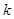 ,使得
,使得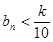 对任意正整数
对任意正整数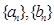 中,对任意
中,对任意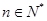 都有:
都有: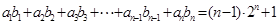 .
.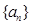 是等差数列,数列
是等差数列,数列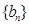 是否为等比数列?若是,请求出通项公式,若不是,请说明理由;
是否为等比数列?若是,请求出通项公式,若不是,请说明理由;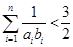 .
.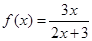 ,数列
,数列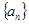 满足
满足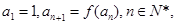
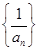 是等差数列;
是等差数列;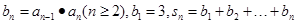 ,若
,若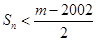 对一切
对一切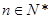 成立,求最小正整数
成立,求最小正整数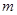 .
.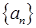 的前
的前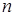 项和
项和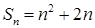 ,设数列
,设数列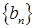 满足
满足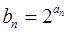 ,
,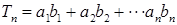 ,求
,求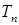
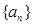 的前n项和为
的前n项和为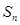 ,若
,若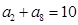 ,
,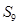 等于( )
等于( ) 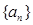 中,
中,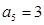 ,
,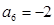 ,则
,则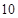 项和
项和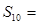 __________
__________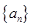 ,如果存在实常数
,如果存在实常数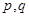 ,使得
,使得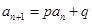 对于任意
对于任意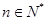 都成立,我们称数列
都成立,我们称数列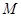 类数列”.
类数列”.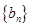 是 “
是 “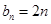 ,求它对应的实常数
,求它对应的实常数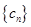 满足
满足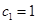 ,
,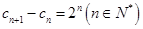 ,求数列
,求数列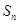 为等差数列
为等差数列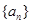 的前
的前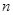 项和.若
项和.若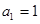 ,公差
,公差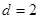 ,
,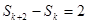 4,则正整数
4,则正整数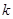 =________.
=________.