题目内容
【题目】某企业生产的一种产品的广告费用
(单位:万元)与销售额
(单位:万元)的统计数据如下表:
广告费用 |
|
|
|
|
|
销售额 |
|
|
|
|
|
（1）根据上述数据，求出销售额
（万元)关于广告费用
（万元)的线性回归方程；
（2）如果企业要求该产品的销售额不少于
万元，则投入的广告费用应不少于多少万元?
（参考数值： 
.
回归直线的斜率和截距的最小二乘法估计公式分别为：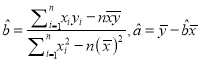 
）
【答案】（1）
（2）投入的广告费用应不少于
万元
【解析】试题分析：（1）由公式
求得
的值，再根据表格数据先求出样本的中心点坐标，代入回归方程可求得
的值即可确定线性回归方程；（2）根据回归方程，由
可得结果.
试题解析：（1）由表格数据可得 
， 
， 
， 
所求回归直线方程为
.
（2）
（万元）.
答：投入的广告费用应不少于
万元.
【方法点晴】本题主要考查线性回归方程及其应用，属于中档题.求回归直线方程的步骤：①依据样本数据画出散点图，确定两个变量具有线性相关关系；②计算
的值；③计算回归系数
；④写出回归直线方程为
；(2) 回归直线过样本点中心
是一条重要性质，利用线性回归方程可以估计总体，帮助我们分析两个变量的变化趋势.
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
【题目】（文科）（本小题满分12分）某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本，得频率分布表如下：
组号 | 分组 | 频数 | 频率 |
第一组 | [230，235) | 8 | 0.16 |
第二组 | [235，240) | ① | 0.24 |
第三组 | [240，245) | 15 | ② |
第四组 | [245，250) | 10 | 0.20 |
第五组 | [250，255] | 5 | 0.10 |
合 计 | 50 | 1.00 | |
（1）写出表中①②位置的数据；
（2）为了选拔出更优秀的学生，高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核，分别求第三、四、五各组参加考核人数；
（3）在（2）的前提下，高校决定在这6名学生中录取2名学生，求2人中至少有1名是第四组的概率．
