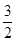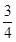题目内容
一个圆柱的侧面积展开图是一个正方形,这个圆柱的全面积与侧面积的比是( )
A.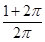 | B.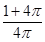 | C.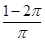 | D.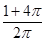 |
A
解析试题分析:设圆柱底面积半径为r,则高为2πr,那么根据圆柱体的侧面积就是矩形的面积,全面积加上两个底面的面积得到,故有全面积:侧面积=[(2πr)2+2πr2]:(2πr)2
=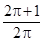 ,故选A.
,故选A.
考点:本题主要考查了圆柱的侧面积、表面积,考查计算能力,是基础题.
点评:解决该试题的关键是设圆柱底面积半径为r,求出圆柱的高,然后求圆柱的全面积与侧面积的比.

练习册系列答案
相关题目
如图⑴、⑵、⑶、⑷为四个几何体的三视图,根据三视图可以判断这四个几何体依次分别为
| A.三棱台、三棱柱、圆锥、圆台 | B.三棱台、三棱锥、圆锥、圆台 |
| C.三棱柱、正四棱锥、圆锥、圆台 | D.三棱柱、三棱台、圆锥、圆台 |
正方体的内切球,与各棱相切的球,外接球的体积之比为( )
| A.1:2:3 | B.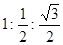 | C.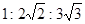 | D.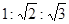 |
正方体的棱长为 ,由它的互不相邻的四个顶点连线所构成的四面体的体积是( )
,由它的互不相邻的四个顶点连线所构成的四面体的体积是( )
A. | B.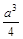 | C. | D. |
下列几何体中是旋转体的是
①圆柱;②六棱锥;③正方体;④球体;⑤四面体.
| A.①和⑤ | B.① | C.③和④ | D.①和④ |
把正方形 沿对角线
沿对角线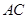 折起,当以
折起,当以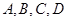 四点为顶点的三棱锥体积最大时,直线
四点为顶点的三棱锥体积最大时,直线 和平面
和平面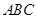 所成的角的大小为( )
所成的角的大小为( )
A.90 | B.30 | C.60 | D.45 |
某几何体的三视图如图所示,则该几何体的体积是( )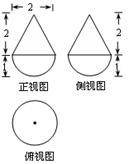
A. | B.2? | C.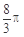 | D. |
已知正四棱锥 中,
中, ,那么当该棱锥的体积最大时,它的高为
,那么当该棱锥的体积最大时,它的高为
( )
| A.1 | B. | C.2 | D.3 |
 是边长为
是边长为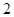 的正三角形,俯视图为正六边形,那么该几何体的左视图的面积为
的正三角形,俯视图为正六边形,那么该几何体的左视图的面积为