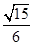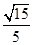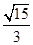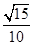题目内容
如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )
A.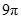 | B.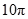 | C.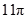 | D.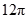 |
D
解析试题分析:由三视图可知,该几何体是下部为圆柱体,上部是半径为1的球,直接求表面积即可。
由三视图容易推知几何体是:上部是半径为1的球,下部是底面直径为2的圆柱体,高为3,该几何体的表面积为:3 2π+2π+4πr2=12π,故答案为:12π,故选D.
2π+2π+4πr2=12π,故答案为:12π,故选D.
考点:本题考查三视图、组合体的表面积.考查简单几何体的三视图的运用;培养同学们的空间想象能力和基本的运算能力;中档题.
点评:解决该试题的关键是将三视图还原为几何体。

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
正方体的棱长为 ,由它的互不相邻的四个顶点连线所构成的四面体的体积是( )
,由它的互不相邻的四个顶点连线所构成的四面体的体积是( )
A. | B.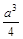 | C. | D. |
把正方形 沿对角线
沿对角线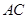 折起,当以
折起,当以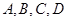 四点为顶点的三棱锥体积最大时,直线
四点为顶点的三棱锥体积最大时,直线 和平面
和平面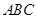 所成的角的大小为( )
所成的角的大小为( )
A.90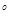 | B.30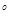 | C.60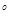 | D.45 |
正三棱柱 的各棱长都是2,E,F分别是
的各棱长都是2,E,F分别是 的中点,则EF的长是( )
的中点,则EF的长是( )
| A.2 | B. | C. | D. |
某几何体的三视图如图所示,则该几何体的体积是( )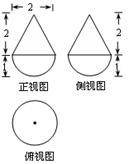
A. | B.2? | C.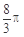 | D. |
长方体 的各个顶点都在表面积为
的各个顶点都在表面积为 的球
的球 的球面上,其中
的球面上,其中 ,则四棱锥
,则四棱锥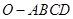 的体积为
的体积为
A. | B. | C. | D. |
某几何体的三视图如右图所示,则其侧面积为 
A. | B. | C. | D. |
在棱柱中满足 ( )
| A.只有两个面平行 | B.所有面都平行 |
| C.所有面都是平行四边形 | D.两对面平行,且各侧棱也相互平行 |
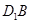 所成角的余弦值为()
所成角的余弦值为()