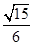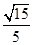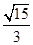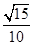题目内容
已知某个几何体的三视图如右图所示,根据图中标出的数字,得这个几何体的体积是( )
A. | B.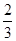 | C. | D.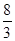 |

C.
解析试题分析:由三视图可知此几何体为三棱锥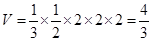 .
.
考点:空间几何体的三视图.
点评:掌握空间几何体的三视图中各视图中数据与几何体对应量之间的关系是解题的关键,要通过作图,识图提高自己的空间想象能力.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
右图是底面半径为1,母线长均为2的圆锥和圆柱的组合体,则该组合体的侧视图的面积为( )
A. | B.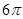 | C. | D. |
一个棱锥的三视图如图,则该棱锥的全面积(单位:cm2)为( ) 
A.36+12 | B.48+24 | C.48+12 | D.36+24 |
如图⑴、⑵、⑶、⑷为四个几何体的三视图,根据三视图可以判断这四个几何体依次分别为
| A.三棱台、三棱柱、圆锥、圆台 | B.三棱台、三棱锥、圆锥、圆台 |
| C.三棱柱、正四棱锥、圆锥、圆台 | D.三棱柱、三棱台、圆锥、圆台 |
正方体的棱长为 ,由它的互不相邻的四个顶点连线所构成的四面体的体积是( )
,由它的互不相邻的四个顶点连线所构成的四面体的体积是( )
A. | B.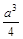 | C. | D. |
长方体 的各个顶点都在表面积为
的各个顶点都在表面积为 的球
的球 的球面上,其中
的球面上,其中 ,则四棱锥
,则四棱锥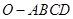 的体积为
的体积为
A. | B. | C. | D. |
 与
与 是异面直线的是 ……………………………………………( )
是异面直线的是 ……………………………………………( )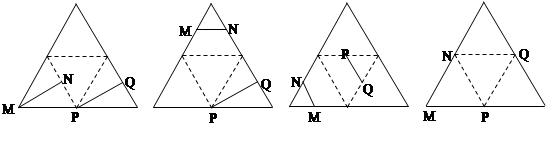
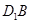 所成角的余弦值为()
所成角的余弦值为()