题目内容
6.已知抛物线C:y2=2px(p>0),其焦点F到其准线的距离为$\frac{1}{2}$,过焦点F且倾斜角为45°的直线l交抛物线C于A,B两点,求:(1)抛物线C的方程及其焦点坐标;
(2)|AB|.
分析 (1)由抛物线的焦点F到其准线的距离为$\frac{1}{2}$,得到p=$\frac{1}{2}$,则抛物线方程可求;
(2)写出直线l的方程,联立直线方程和抛物线方程,利用根与系数的关系求得A,B的横坐标的和,代入抛物线的弦长公式得答案.
解答 解:(1)∵抛物线C:y2=2px(p>0)的焦点F到其准线的距离为$\frac{1}{2}$,即p=$\frac{1}{2}$,
∴抛物线C的方程为y2=x.
焦点坐标为($\frac{1}{4},0$);
(2)过焦点F且倾斜角为45°的直线l的方程为y=x-$\frac{1}{4}$,
联立$\left\{\begin{array}{l}{y=x-\frac{1}{4}}\\{{y}^{2}=x}\end{array}\right.$,得16x2-24x+1=0.
设A(x1,y1),B(x2,y2),
则${x}_{1}+{x}_{2}=\frac{24}{16}=\frac{3}{2}$,
∴|AB|=${x}_{1}+{x}_{2}+p=\frac{3}{2}+\frac{1}{2}=2$.
点评 本题考查了抛物线的方程,考查了直线与抛物线的关系,训练了弦长公式的应用,是中档题.

练习册系列答案
相关题目
15.若集合M={y|y=x2+1},N={x|y=x+1},则M∩N=( )
| A. | {(0,1)} | B. | [1,+∞) | C. | {(0,1),(1,2)} | D. | {y|y>1} |
14.设a为实数,函数f(x)=x3+ax2+(a-2)x的导数是f′(x),且f′(x)是偶函数,则曲线y=f(x)在原点处的切线方程为( )
| A. | y=-2x | B. | y=3x | C. | y=-3x | D. | y=4x |
10.sin245°sin125°+sin155°sin35°的值是( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
 中,底面
中,底面 是直角梯形,
是直角梯形, ,
, ,侧面
,侧面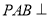 底面
底面 ,
,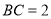 .
.
 平面
平面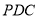 ;
;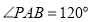 ,求点
,求点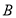 到直线
到直线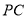 的距离.
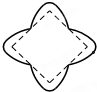
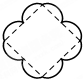
的距离. 如图:一个周长为1的圆沿着边长为2的正方形的边按逆时针方向滚动(无滑动),P是圆上的一定点,开始时PA⊥AB,当圆滚过正方形一周,回到起点时,点P所绘出的图形大致是( )
如图:一个周长为1的圆沿着边长为2的正方形的边按逆时针方向滚动(无滑动),P是圆上的一定点,开始时PA⊥AB,当圆滚过正方形一周,回到起点时,点P所绘出的图形大致是( )