题目内容
15．若集合M={y|y=x2+1}，N={x|y=x+1}，则M∩N=（ ）| A． | {（0，1）} | B． | [1，+∞） | C． | {（0，1），（1，2）} | D． | {y|y＞1} |
分析 化简得集合M={y|y≥1}，N=R，再根据交集定义即得结论．
解答 解：∵集合M={y|y=x2+1}，
∴集合M={y|y≥1}，
∵集合N={x|y=x+1}，
∴集合N=R，
所以M⊆N，从而M∩N=M={y|y≥1}，
故选：B．
点评 本题考查集合的交集运算，属基础题．
练习册系列答案
相关题目
6．关于函数f（x）=log3（-x）和g（x）=3-x，下列说法中正确的是（ ）
| A． | 都是奇函数 | B． | 都是偶函数 | C． | 函数f（x）的值域为R | D． | 函数g（x）的值域为R |
20．
如图是用计算机随机模拟的方法估计概率的程序框图，P表示估计结果，则输出P的近似值为（ ）
如图是用计算机随机模拟的方法估计概率的程序框图，P表示估计结果，则输出P的近似值为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{3}{4}$ | D． | $\frac{7}{8}$ |
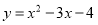的定义域为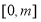
，值域为
，则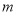
的取值范围是（ ）
B．
D．