题目内容
13.已知集合M={x|x2-2x-3>0},N={x|ax2+x+b≥0,a≠0},若∁RM=N,则a+b等于( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 先花简集合M,再求出集合M的补集,再根据韦达定理即可求出a,b的值,问题得以解决.
解答 解:∵集合M={x|x2-2x-3>0}={x|x>3或x<-1},
故N=∁UM=[-1,3];
故$\left\{\begin{array}{l}{a<0}\\{-1+3=-\frac{1}{a}}\\{-1•3=\frac{b}{a}}\end{array}\right.$,
解得,a=-$\frac{1}{2}$,b=$\frac{3}{2}$;
故a+b=1;
故选:B
点评 本题考查了集合的化简与运算及二次不等式的应用,属于基础题

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
2.从标有1,2,3,4,5,6的6张纸片中任取2张,那么这2张纸片数字之积为6的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{15}$ | C. | $\frac{2}{15}$ | D. | $\frac{1}{3}$ |
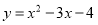 的定义域为
的定义域为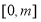 ,值域为
,值域为 ,则
,则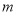 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.
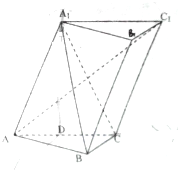 已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,BA1⊥AC1.
已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,BA1⊥AC1.