题目内容
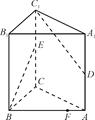
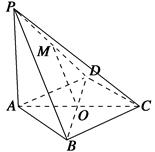
如图四棱锥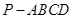 中,底面
中,底面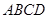 是平行四边形,
是平行四边形,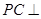 平面
平面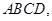
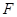 是
是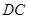 的中点,
的中点,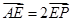 .
.
(1)试判断直线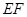 与平面
与平面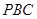 的位置关系,并予以证明;
的位置关系,并予以证明;
(2)若四棱锥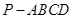 体积为
体积为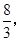
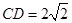 ,
,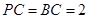 ,求证:平面
,求证:平面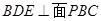 .
.
(1)参考解析;(2)参考解析
解析试题分析:(1)由题意判断直线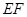 与平面
与平面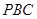 的位置关系,这类题型要转化为直线EF与平面内一条直线平行或则相交,所以转化为平面内两条直线的位置关系.通过作出直线EG即可得到直线EF与直线CG是相交的,即可得到结论.
的位置关系,这类题型要转化为直线EF与平面内一条直线平行或则相交,所以转化为平面内两条直线的位置关系.通过作出直线EG即可得到直线EF与直线CG是相交的,即可得到结论.
(2)平面与平面垂直关键是要转化为直线与平面的垂直,通过研究底面平行四边形的边的大小即可得到BD垂直于BC.即可得到结论.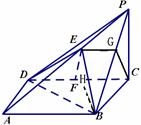
试题解析:(1)直线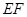 与平面
与平面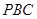 相交.
相交.
证明如下:过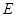 作
作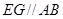 交
交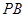 于
于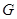 ,
,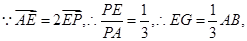
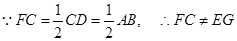
由底面 是平行四边形得
是平行四边形得 ,
, 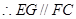
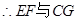 相交,故直线
相交,故直线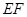 与平面
与平面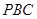 相交.
相交.
(2)解:过B作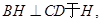
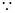 四棱锥
四棱锥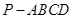 体积为
体积为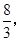
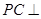 平面
平面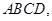

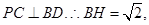
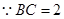
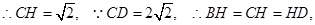
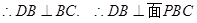 ,
, 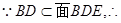 平面
平面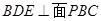
考点:1.线面的位置关系.2.面面的位置关系.3.空间想象力.

练习册系列答案
相关题目
 中,已知
中,已知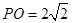 ,
,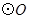 的直径
的直径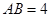 ,点
,点 在底面圆周上,且
在底面圆周上,且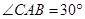 ,
,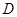 为
为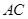 的中点.
的中点.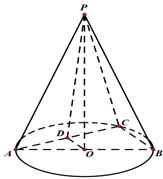
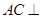 平面
平面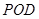 ;
; 到面
到面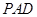 的距离.
的距离.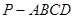 中,底面
中,底面 为矩形,
为矩形, 平面
平面 ,
, 为
为 中点.
中点.
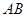 //平面
//平面 ;
; 平面
平面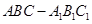 中,点
中,点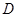 是
是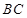 上一点.
上一点.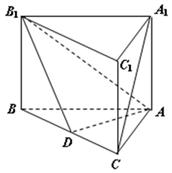
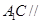 平面
平面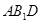 ;
;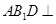 平面
平面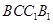 ,求证
,求证 .
.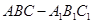 的侧棱与底面垂直,
的侧棱与底面垂直,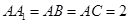 ,
,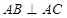 , M、N分别是
, M、N分别是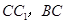 的中点,点P在线段
的中点,点P在线段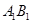 上,且
上,且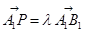 ,
,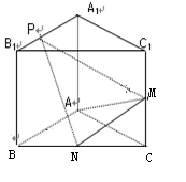
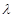 取何值,总有
取何值,总有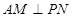 .
.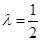 时,求平面
时,求平面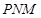 与平面
与平面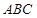 所成锐二面角的余弦值.
所成锐二面角的余弦值.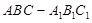 中,
中,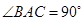 ,
,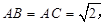
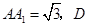 是
是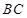 中点,
中点,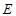 是
是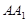 中点.
中点.
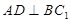 ;
;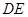 ∥面
∥面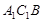 .
.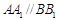 ,
,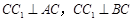 .
.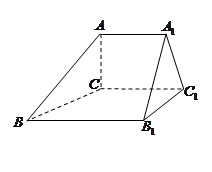
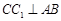 ;
;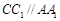 .
.
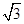 时,求PB的长.
时,求PB的长.