Question

【题目】如图，已知四棱锥P﹣ABCD的底面ABCD为菱形，且∠ABC=60°，
AB=PC=2，PA=PB= ．

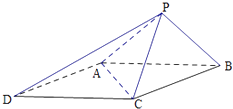
（1）求证：平面PAB⊥平面ABCD；
（2）设H是PB上的动点，求CH与平面PAB所成最大角的正切值．

Answer 1

【答案】
（1）

证明：取AB中点O，连结PO、CO，

∵PA=PB= ，AB=2，∴△PAB为等腰直角三角形，

∴PO=1，PO⊥AB，

∵AB=BC=2，∠ABC=60°，∴△ABC为等边三角形，

∴ ，又PC=2，

∴PO2+CO2=PC2，∴PO⊥CO，

又AB∩CO=O，AB平面ABCD，CO平面ABCD，

∴PO⊥平面ABC，又PO平面PAB，

∴平面PAB⊥平面ABCD．

（2）

解：∵平面PAB⊥平面ABCD，平面PAB∩平面ABCD=AB，OC⊥AB，OC平面ABCD，

∴OC⊥平面PAB，

∴∠CHO为CH与平面PAB所成的角．

∵tan∠CHO= ，∴当OH⊥PB时，OH取得最小值，此时tan∠CHO取得最大值．

当OH⊥PB时，OH= = ．

∴tan∠CHO= = ．

【解析】（1）取AB中点O，连结PO、CO，由PA=PB可得PO⊥AB，利用特殊三角形的性质计算PO，OC，PC，可证PO⊥OC，于是PO⊥平面ABCD，故平面PAB⊥平面ABCD；（2）由面面垂直的性质可知∠CHO为CH与平面PAB所成的角，故当OH最小值，tan∠CHO= 取得最大值．
【考点精析】本题主要考查了平面与平面垂直的判定和空间角的异面直线所成的角的相关知识点，需要掌握一个平面过另一个平面的垂线，则这两个平面垂直；已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则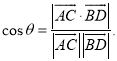才能正确解答此题．