题目内容
【题目】设函数f(x)=x2﹣ax+a+3,g(x)=ax﹣2a.
(1)若函数h(x)=f(x)﹣g(x)在[﹣2,0]上有两个零点,求实数a的取值范围;
(2)若存在x0∈R,使得f(x0)≤0与g(x0)≤0同时成立,求实数a的最小值.
【答案】
(1)
解:由已知,h(x)=f(x)﹣g(x)=x2﹣2ax+3a+3=0在[﹣2,0]上有两个不同的实数解,
所以 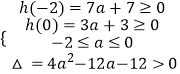 ,
,
即 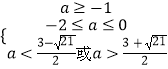 ,
,
解得 ![]() ,
,
(2)
解:由已知, ![]() ,
,
(1)+(2)得 ![]() ,得a≥3,
,得a≥3,
再由(2)得x0≤2,由(1)得 ![]() ,得x0>1,
,得x0>1,
于是,问题等价于:a≥3,且存在x0∈(1,2]满足 ![]() ,
,
令t=x0﹣1∈(0,1], ![]() ,
,
因为 ![]() 在(0,1]上单调递减,
在(0,1]上单调递减,
所以φ(t)≥φ(1)=7,即a≥7,
故实数a的最小值为7.
【解析】(1)由h(x)在区间内的两个零点,结合图形,得到需要满足的条件.(2)由f(x0)≤0与g(x0)≤0同时成立,得到得a≥3,可将问题转化为最值问题,由单调性得到最值,即可.

练习册系列答案
相关题目
【题目】若学生![]() 一天学习数学超过两个小时的概率为
一天学习数学超过两个小时的概率为![]() (每天是相互独立没有影响的),一周内至少有四天每天学习数学超过两个小时,就说该生本周数学学习是投入的.
(每天是相互独立没有影响的),一周内至少有四天每天学习数学超过两个小时,就说该生本周数学学习是投入的.
(Ⅰ)①设学生![]() 本周一天学习数学超过两个小时的天数为
本周一天学习数学超过两个小时的天数为![]() 求
求![]() 的分布列与数学期望
的分布列与数学期望![]()
②求学生![]() 本周数学学习投入的概率.
本周数学学习投入的概率.
(Ⅱ)为了研究学生学习数学的投入程度和本周数学周练成绩的关系,随机在年级中抽取了![]() 名学生进行调查,所得数据如下表所示:
名学生进行调查,所得数据如下表所示:
成绩理想 | 成绩不太理想 | 合计 | |
数学学习投入 | 20 | 10 | 30 |
数学学习不太投入 | 10 | 15 | 25 |
合计 | 30 | 25 | 55 |
根据上述数据能否有![]() 的把握认为“学生学习数学的投入程度和本周数学成绩两事件有关”?
的把握认为“学生学习数学的投入程度和本周数学成绩两事件有关”?
附:![]()
|
|
|
|
|
|
|
|
|
|
| 10.828 |