题目内容
已知函数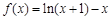 .
.
(1)求函数 的单调递减区间;
的单调递减区间;
(2)若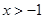 ,证明:
,证明: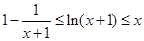 .
.
(1)(0,+∞)(2)由⑴知,当x∈(-1,0)时,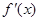 >0,当x∈(0,+∞)时,
>0,当x∈(0,+∞)时,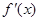 <0,因此,当
<0,因此,当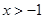 时,
时, ≤
≤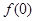 ,即
,即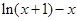 ≤0∴
≤0∴ 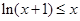 .
.
令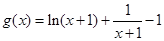 ,则
,则 =
=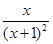 ∴ 当x∈(-1,0)时,
∴ 当x∈(-1,0)时,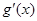 <0,当x∈(0,+∞)时,
<0,当x∈(0,+∞)时,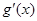 >0.∴ 当
>0.∴ 当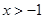 时,
时,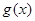 ≥
≥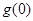 ,即
,即 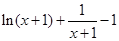 ≥0,∴
≥0,∴  综上可知,当
综上可知,当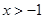 时,有
时,有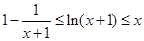
解析试题分析:⑴函数f(x)的定义域为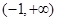 .
.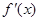 =
=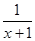 -1=-
-1=-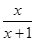 .
.
由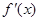 <0及x>-1,得x>0.∴ 当x∈(0,+∞)时,f(x)是减函数,即f(x)的单调递减区间为(0,+∞).
<0及x>-1,得x>0.∴ 当x∈(0,+∞)时,f(x)是减函数,即f(x)的单调递减区间为(0,+∞).
⑵证明:由⑴知,当x∈(-1,0)时,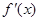 >0,当x∈(0,+∞)时,
>0,当x∈(0,+∞)时,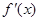 <0,
<0,
因此,当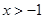 时,
时, ≤
≤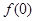 ,即
,即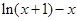 ≤0∴
≤0∴ 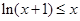 .
.
令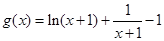 ,则
,则 =
=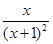 .……………8分
.……………8分
∴ 当x∈(-1,0)时,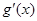 <0,当x∈(0,+∞)时,
<0,当x∈(0,+∞)时,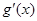 >0.
>0.
∴ 当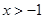 时,
时,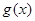 ≥
≥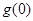 ,即
,即 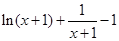 ≥0,∴
≥0,∴  .
.
综上可知,当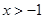 时,有
时,有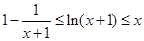 .……………………………………12分
.……………………………………12分
考点:求函数单调区间及证明不等式
点评:求单调区间时首先确定其定义域,第二问将证明不等式问题转化为求函数最值问题,进而可利用导数通过求其最值确定不等式的正确性

练习册系列答案
相关题目
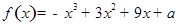 在区间[-2,2]的最大值为20,求它在该区间的最小值。
在区间[-2,2]的最大值为20,求它在该区间的最小值。
 的解析式及减区间;
的解析式及减区间; 的最小值。
的最小值。 .
. 的最小值;
的最小值; 都有
都有 ,求实数
,求实数 的取值范围.
的取值范围. .
. 在点
在点 处的切线方程;
处的切线方程; ,如果过点
,如果过点 可作曲线
可作曲线
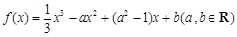
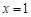 为
为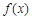 的极值点,求
的极值点,求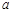 的值;
的值;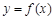 的图象在点
的图象在点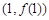 处的切线方程为
处的切线方程为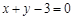 ,求
,求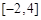 上的最大值;
上的最大值;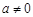 时,若
时,若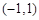 上不单调,求
上不单调,求
 在点
在点 处的切线与直线
处的切线与直线 垂直,求a的值;
垂直,求a的值;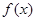 的单调区间;
的单调区间; 是函数
是函数 的一个极值点.
的一个极值点.


 的值;
的值; ,
, 时,证明:
时,证明:
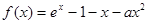
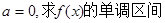 ;
;