题目内容
(本题满分12分)已知 是函数
是函数 的一个极值点.
的一个极值点.


(Ⅰ)求 的值;
的值;
(Ⅱ)当 ,
, 时,证明:
时,证明:
(1)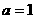 (2)要证明差的绝对值小于等于e,只要证明差介于-e和e之间即可,求解函数的 最值的差可知。
(2)要证明差的绝对值小于等于e,只要证明差介于-e和e之间即可,求解函数的 最值的差可知。
解析试题分析:(Ⅰ)解: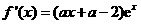 , 2分
, 2分
由已知得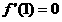 ,解得
,解得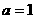 .
.
当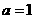 时,
时,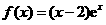 ,在
,在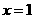 处取得极小值.
处取得极小值.
所以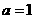 . 4分
. 4分
(Ⅱ)证明:由(Ⅰ)知,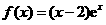 ,
,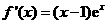 .
.
当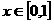 时,
时,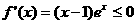 ,
,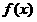 在区间
在区间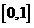 单调递减;
单调递减;
当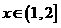 时,
时,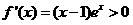 ,
,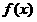 在区间
在区间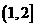 单调递增.
单调递增.
所以在区间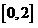 上,
上,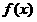 的最小值为
的最小值为 . 8分
. 8分
又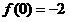 ,
,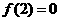 ,
,
所以在区间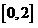 上,
上,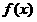 的最大值为
的最大值为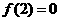 . 10分
. 10分
对于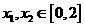 ,有
,有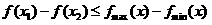 .
.
所以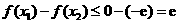 . 12分
. 12分
考点:函数的最值
点评:解决的关键是利用导数判定单调性,并能结合函数的最值来证明不等式,属于中档题。

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
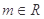 ,函数
,函数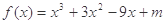 .
.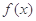 的极值(用含
的极值(用含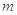 的式子表示);
的式子表示);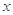 轴有3个不同交点,求
轴有3个不同交点,求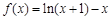 .
. 的单调递减区间;
的单调递减区间;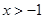 ,证明:
,证明: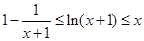 .
.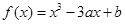 在
在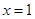 处有极小值
处有极小值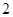 。
。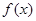 的解析式;
的解析式;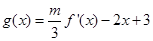 在
在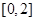 只有一个零点,求
只有一个零点,求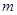 的取值范围。
的取值范围。 在
在 处取得极值,并且它的图象与直线
处取得极值,并且它的图象与直线 在点( 1 , 0 ) 处相切, 求a , b , c的值.
在点( 1 , 0 ) 处相切, 求a , b , c的值.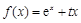 (e为自然对数的底数).
(e为自然对数的底数).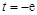 时,求函数
时,求函数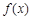 的单调区间;
的单调区间; ,不等式
,不等式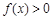 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围. (a>0),g(x)=2lnx+bx且直线y=2x-2与曲线y=g(x)相切.
(a>0),g(x)=2lnx+bx且直线y=2x-2与曲线y=g(x)相切. )内的一切实数x,小等式f(x)≥g(x)恒成立,求实数a的取值范围;
)内的一切实数x,小等式f(x)≥g(x)恒成立,求实数a的取值范围; 成立;
成立; .
.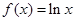 ,
,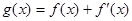 .
.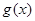 的单调区间和最小值;
的单调区间和最小值;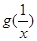 的大小关系;
的大小关系;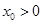 ,使得
,使得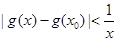 对任意
对任意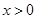 成立?若存在,求出
成立?若存在,求出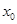 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.