题目内容
已知函数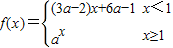
在（-∞，+∞）上单调递减，那么实数a的取值范围是（ ）A．（0，1）
B．
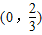
C．
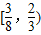
D．
【答案】分析：f（x）在（-∞，+∞）上单调递减，即f（x）在两段上都单调递减，且在x＜1时，x→1时，f（x）≥f（1）．
解答：解：x＜1时，f（x）=（3a-2）x+6a-1单调递减，故3a-2＜0，a＜
，
且x→1时，f（x）→9a-3≥f（1）=a，a≥
；
x＞1时，f（x）=ax单调递减，故0＜a＜1，综上所述，a的范围为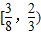
故选C
点评：本题考查分段函数的单调性，除了考虑各段的单调性，还要注意断开点处的情况．
解答：解：x＜1时，f（x）=（3a-2）x+6a-1单调递减，故3a-2＜0，a＜
，且x→1时，f（x）→9a-3≥f（1）=a，a≥
；x＞1时，f（x）=ax单调递减，故0＜a＜1，综上所述，a的范围为
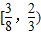
故选C
点评：本题考查分段函数的单调性，除了考虑各段的单调性，还要注意断开点处的情况．
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目