题目内容
已知函数在R上可导,且f′(-1)=2,则
=( )
| lim |
| △x→0 |
| f(-1-△x)-f(-1) |
| △x |
分析:根据导数的几何意义可知f′(-1)=
=2,从而求出所求.
| lim |
| △x→0 |
| f(-1-△x)-f(-1) |
| -△x |
解答:解:∵f′(-1)=2
∴f′(-1)=
=2
即
=-2
故选D.
∴f′(-1)=
| lim |
| △x→0 |
| f(-1-△x)-f(-1) |
| -△x |
即
| lim |
| △x→0 |
| f(-1-△x)-f(-1) |
| △x |
故选D.
点评:本题主要考查了函数的导数,以及导数的几何意义,解题的关键是理解导数的定义,属于基础题.

练习册系列答案
相关题目
 在R上可导,且
在R上可导,且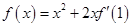 ,则
,则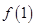 与
与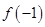 的大小关系是( )
的大小关系是( )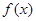 在R上可导,且
在R上可导,且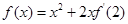 ,则
,则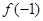 与
与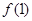 的大小为( )
的大小为( )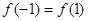 B.
B.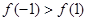
 D.不确定
D.不确定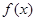 在R上可导,且
在R上可导,且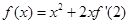 ,则
,则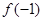 与
与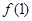 的大小关系为 ( )
的大小关系为 ( )
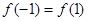 B.
B.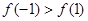 C.
C.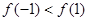 D.不确定
D.不确定 在R上可导,函数
在R上可导,函数 给出以下四个命题:
给出以下四个命题: (2)
(2) (3)
(3) (4)
(4) 的图象关于原点对称,其中正确的命题序号有__________
的图象关于原点对称,其中正确的命题序号有__________