题目内容
【题目】设椭圆C:![]() (a>b>0)的右焦点为F,椭圆C上的两点A,B关于原点对称,且满足
(a>b>0)的右焦点为F,椭圆C上的两点A,B关于原点对称,且满足![]() ,|FB|≤|FA|≤2|FB|,则椭圆C的离心率的取值范围是( )
,|FB|≤|FA|≤2|FB|,则椭圆C的离心率的取值范围是( )
A.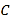 B.
B.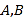
C.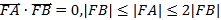 D.
D.![]()
【答案】A
【解析】
设椭圆左焦点为![]() ,由椭圆的对称性可知且
,由椭圆的对称性可知且![]() ,可得四边形AFBF′为矩形,设|AF′|=n,|AF|=m,根据椭圆的定义以及题意可知mn=2b2 ,从而可求得
,可得四边形AFBF′为矩形,设|AF′|=n,|AF|=m,根据椭圆的定义以及题意可知mn=2b2 ,从而可求得![]() 的范围,进而可求得离心率.
的范围,进而可求得离心率.
设椭圆左焦点为![]() ,由椭圆的对称性可知,四边形
,由椭圆的对称性可知,四边形![]() 为平行四边形,
为平行四边形,
又![]() ,即FA⊥FB,故平行四边形AFBF′为矩形,所以|AB|=|FF′|=2c.
,即FA⊥FB,故平行四边形AFBF′为矩形,所以|AB|=|FF′|=2c.
设|AF′|=n,|AF|=m,则在Rt△F′AF中,
m+n=2a ①,m2+n2=4c2 ②,
联立①②得mn=2b2 ③.
②÷③得![]() ,令
,令![]() =t,得t+
=t,得t+![]() .
.
又由|FB|≤|FA|≤2|FB|得![]() =t∈[1,2],所以t+
=t∈[1,2],所以t+![]() ∈
∈![]() .
.
故椭圆C的离心率的取值范围是 .
.
故选:A

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目