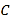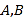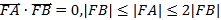题目内容
【题目】已知函数f(x)=![]()
(1)求f(x)>0的解集;
(2)若x∈R时,![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
【答案】(1)(0,+∞)(2)[![]() ,+∞)
,+∞)
【解析】
(1)通过对f(x)求导,可得x∈R时,f′(x)≥0,所以f(x)在(﹣∞,+∞)上单调递增,又f(0)=0,x∈(0,+∞)时f(x)>0,不等式得解;
(2)若x∈R时,![]() 恒成立,不等式转化为2e
恒成立,不等式转化为2e![]() ex
ex![]() (x∈R),因为都是偶函数,所以只需x∈[0,+∞)时,2e
(x∈R),因为都是偶函数,所以只需x∈[0,+∞)时,2e![]() e2x﹣1≥0成立即可,构造新的函数F(x)=2e
e2x﹣1≥0成立即可,构造新的函数F(x)=2e![]() e2x﹣1,求导后再对导函数进行分类讨论,可得实数m的取值范围.
e2x﹣1,求导后再对导函数进行分类讨论,可得实数m的取值范围.
(1)因为f(x)=![]() ,则f′(x)=
,则f′(x)=![]() ;
;
所以x∈R时,f′(x)≥0,
所以f(x)在(﹣∞,+∞)上单调递增,又f(0)=0,
所以x∈(﹣∞,0)时,f(x)<0,
x∈(0,+∞)时f(x)>0,
∴f(x)>0的解集为(0,+∞).
(2)因为x∈R时,2e![]() e2x+1恒成立,
e2x+1恒成立,
等价于![]() 恒成立,
恒成立,
即2e![]() ex
ex![]() (x∈R),
(x∈R),
因为都是偶函数,
所以只需x∈[0,+∞)时,2e![]() e2x﹣1≥0成立即可,
e2x﹣1≥0成立即可,
令F(x)=2e![]() e2x﹣1,F(0)=0,
e2x﹣1,F(0)=0,
F′(x)=2(2mx+1)e![]() 2e2x=2e2x[(2mx+1)e
2e2x=2e2x[(2mx+1)e![]() 1],F′(0)=0,
1],F′(0)=0,
令G(x)=(2mx+1)e![]() 1,G(0)=0,
1,G(0)=0,
G′(x)=2me![]() (2mx+1)(2mx﹣1)e
(2mx+1)(2mx﹣1)e![]() (4m2x2+2m﹣1)e
(4m2x2+2m﹣1)e![]()
①当2m﹣1≥0,即m![]() 时,G′(x)≥0,所以G(x)在[0,+∞)上单调递增,
时,G′(x)≥0,所以G(x)在[0,+∞)上单调递增,
又因为G(0)=0,所以x∈[0,+∞)时,G(x)≥0,即F′(x)≥0,
所以F(x)在[0,+∞)上单调递增,又因为F(0)=0,所以x∈[0,+∞)时,F(x)≥0,所以m![]() 时满足要求;
时满足要求;
②当m=0,x=1时,2e<e2+1,不成立,所以m≠0;
③当2m﹣1<0且m≠0时,即m![]() 且m≠0时,x∈
且m≠0时,x∈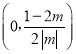 上单调递减,
上单调递减,
又因为G(0)=0,所以x∈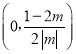 时,G(x)<0,即F′(x)<0,
时,G(x)<0,即F′(x)<0,
所以F(x)在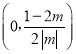 上单调递减,
上单调递减,
又因为F(0)=0,所以x∈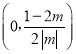 时,F(x)<0,
时,F(x)<0,
所以m![]() 且m≠0时不满足要求.
且m≠0时不满足要求.
综上所述,实数m的取值范围是[![]() ,+∞).
,+∞).