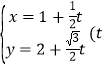题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 在区间
在区间![]() 的最大值;
的最大值;
(2)若函数![]() 有两个极值点
有两个极值点![]() ,求证:
,求证:![]() .
.
【答案】(1)当![]() 时,
时,![]() 的最大值为
的最大值为![]() ;当
;当![]() 时,
时,![]() 的最大值为
的最大值为![]() ;(2)证明见解析;
;(2)证明见解析;
【解析】
(1)求导,对参数进行分类讨论,由函数单调性即可容易求得最值;
(2)根据极值点的定义,求得![]() 之间的关系以及参数
之间的关系以及参数![]() 的范围,构造函数
的范围,构造函数![]() ,将问题转化为求该函数的最值问题,再进行适当放缩即可证明.
,将问题转化为求该函数的最值问题,再进行适当放缩即可证明.
(1)由已知得![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,![]() 的最大值为
的最大值为![]() .
.
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 单调递减,
单调递减,
![]() 的最大值为
的最大值为![]() .
.
综上,当![]() 时,
时,![]() 的最大值为
的最大值为![]() ,
,
当![]() 时,
时,![]() 的最大值为
的最大值为![]() .
.
(2)![]() ,则
,则![]() 的定义域为
的定义域为![]() ,
,
![]()
![]() .
.
若![]() 有两个极值点
有两个极值点![]()
![]() ,则方程
,则方程![]() 的判别式
的判别式![]()
且![]() ,因而
,因而![]() ,
,
又![]() ,∴
,∴![]() ,即
,即![]() ,
,
![]()
![]()
设![]() ,其中
,其中![]() ,
,
由![]() 得
得![]() ,由于
,由于![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
即![]() 的最大值为
的最大值为![]() ,
,
从而![]() 成立.
成立.

练习册系列答案
相关题目
【题目】2017年冬,北京雾霾天数明显减少,据环保局统计三个月的空气质量,达到优良的天数超过![]() 天,重度污染的天数仅有
天,重度污染的天数仅有![]() 天,主要原因是政府对治理雾霾采取有效措施.如:(1)减少机动车尾气排放(2)实施煤改电或煤改气工程(3)关停了大量的排污企业(4)部分企业季节性停产.为了解农村地区实施煤改气工程后天然气的使用从某乡镇随机抽取
天,主要原因是政府对治理雾霾采取有效措施.如:(1)减少机动车尾气排放(2)实施煤改电或煤改气工程(3)关停了大量的排污企业(4)部分企业季节性停产.为了解农村地区实施煤改气工程后天然气的使用从某乡镇随机抽取![]() 户,进行月均用气量调查,得到的用气量数据均在区间
户,进行月均用气量调查,得到的用气量数据均在区间![]() 内,表如下
内,表如下
分组 | 频数 | 频率 |
| 14 | 0.14 |
|
|
|
| 55 | 0.55 |
| 4 | 0.04 |
| 2 | 0.02 |
合计 | 100 | 1 |
(1)求![]() 和
和![]() 值,若同组内的每个数据用该组区间中点值代替,估计该乡镇每户平均用气量;
值,若同组内的每个数据用该组区间中点值代替,估计该乡镇每户平均用气量;
(2)从样本调查的用气量![]() 和
和![]() 的用户组中任选2户,进行燃气使用满意度调查,求2户用气量处于不同区间的概率.
的用户组中任选2户,进行燃气使用满意度调查,求2户用气量处于不同区间的概率.