题目内容
已知直线 过点
过点
(1)若直线 在坐标轴上的截距相等,求直线
在坐标轴上的截距相等,求直线 的方程;
的方程;
(2)若直线 与坐标轴的正半轴相交,求使直线
与坐标轴的正半轴相交,求使直线 在两坐标轴上的截距之和最小时,直线
在两坐标轴上的截距之和最小时,直线 的方程。
的方程。
(1)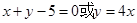 (2)
(2)
解析试题分析:(1)当截距为零时直线为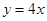 ,当截距不为零时,设直线为
,当截距不为零时,设直线为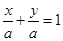 ,代入点
,代入点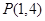 得
得 ,所以直线为
,所以直线为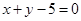 4分
4分
(2) 设所求直线L的方程为:
设所求直线L的方程为: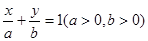
∵直线L经过点P(1,4) ∴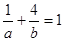
 8分
8分
∴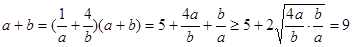 12分
12分
当且仅当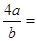
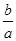 即
即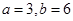 时
时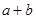 有最小値为9,
有最小値为9,
所求直线方程为 。 14分
。 14分
考点:直线方程
点评:第一问中截距相等要分截距为零与不为零两种情况,第二问中求截距之和的最小值用到了均值不等式,但要注意验证等号成立条件

练习册系列答案
相关题目
 经过直线
经过直线 与直线
与直线 的交点
的交点 ,且垂直于直线
,且垂直于直线 .
.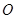 对称的直线方程.
对称的直线方程. 经过两点P1(4,-2)和P2(-1,8)。
经过两点P1(4,-2)和P2(-1,8)。 过点
过点 .
. 、
、 的距离相等时,求直线
的距离相等时,求直线 轴、
轴、 轴围成的三角形的面积为
轴围成的三角形的面积为 时,求直线
时,求直线 ,2)的入射光线 l1
,2)的入射光线 l1 x反射.反射光线l2交y轴于B点,圆C过点A且与l1, l2都相切.
x反射.反射光线l2交y轴于B点,圆C过点A且与l1, l2都相切.
 分别是直线l和圆C上的动点,求
分别是直线l和圆C上的动点,求 的最小值及此时点
的最小值及此时点 的坐标.
的坐标. 中,已知点A(-2,1),直线
中,已知点A(-2,1),直线 。
。 过点A,且与直线
过点A,且与直线 垂直,求直线
垂直,求直线 与直线
与直线 轴、
轴、 轴上的截距之和为3,求直线
轴上的截距之和为3,求直线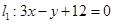 ,
, .求
.求 和
和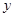 轴所围成的三角形面积.
轴所围成的三角形面积. 与直线
与直线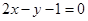 的交点,且与点A(0,4)和点B(4,O)距离相等的直线方程.
的交点,且与点A(0,4)和点B(4,O)距离相等的直线方程.