题目内容
(本小题满分12分)
如图,在平面直角坐标系xOy中,平行于x轴且过点A(3 ,2)的入射光线 l1
,2)的入射光线 l1
被直线l:y= x反射.反射光线l2交y轴于B点,圆C过点A且与l1, l2都相切.
x反射.反射光线l2交y轴于B点,圆C过点A且与l1, l2都相切.
(1)求l2所在直线的方程和圆C的方程;
(2)设 分别是直线l和圆C上的动点,求
分别是直线l和圆C上的动点,求 的最小值及此时点
的最小值及此时点 的坐标.
的坐标.
(1)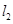 所在的直线方程为
所在的直线方程为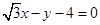 ,圆C的方程为
,圆C的方程为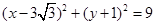 (2)
(2)
解析试题分析:(1)直线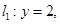 设
设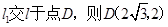 .
.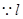 的倾斜角为
的倾斜角为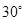 ,
,
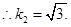
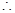 反射光线
反射光线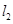 所在的直线方程为
所在的直线方程为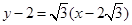 .即
.即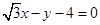 .
.
已知圆C与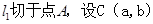 ,
,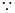 圆心C在过点D且与
圆心C在过点D且与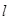 垂直的直线上,
垂直的直线上,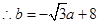 ,又圆心C在过点A且与
,又圆心C在过点A且与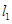 垂直的直线上,
垂直的直线上,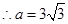 ,
,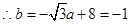 ,圆C的半径r=3,
,圆C的半径r=3,
故所求圆C的方程为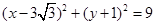 .
.
(2)设点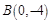 关于
关于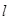 的对称点
的对称点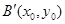 ,
,
则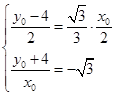 ,得
,得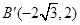 ,
,
固定点Q可发现,当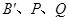 共线时,
共线时,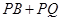 最小,
最小,
故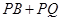 的最小值为
的最小值为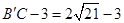 。 …12分
。 …12分
此时由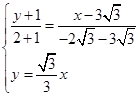 ,得
,得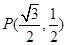 .
.
考点:本小题主要考查直线与圆的方程的应用.
点评:本题主要考查圆标准方程,简单几何性质,直线与圆的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 点射出,到
点射出,到 轴上的
轴上的 点后,被
点后,被 ,求
,求 所在直线的方程及点
所在直线的方程及点 ,求:
,求: 过点
过点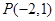 .
. 、
、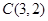 的距离相等时,求直线
的距离相等时,求直线 轴、
轴、 轴围成的三角形的面积为
轴围成的三角形的面积为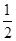 时,求直线
时,求直线 过点
过点
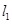 :
: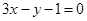 ,
, :
: ,求:
,求: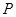 的坐标;(2)过点
的坐标;(2)过点 、
、 到直线
到直线 的距离相等,且直线
的距离相等,且直线 和
和 的交点,求直线
的交点,求直线 :
: 和直线
和直线 :
: .
. 的值.
的值.