题目内容
已知圆心为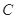 的圆经过点
的圆经过点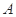 (0,
(0,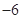 ),
),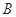 (1,
(1, ),且圆心在直线
),且圆心在直线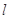 :
: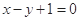 上,求圆心为
上,求圆心为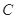 的圆的标准方程.
的圆的标准方程.

解析试题分析:由已知圆心为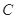 的圆经过点
的圆经过点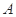 (0,
(0,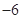 ),
),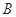 (1,
(1, ),知圆心C在线段AB的垂直平分线上,又圆心在直线
),知圆心C在线段AB的垂直平分线上,又圆心在直线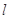 :
: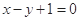 上,写出线段AB的垂直平分线的方程与直线
上,写出线段AB的垂直平分线的方程与直线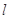 的方程联立方程组就可求出圆心的坐标,再由圆经过点A就可求出其半径,从而就可写出所求圆的方程.
的方程联立方程组就可求出圆心的坐标,再由圆经过点A就可求出其半径,从而就可写出所求圆的方程.
试题解析:因为点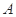 (0,
(0,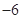 ),
),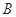 (1,
(1, ),所以线段AB的中点D的坐标为
),所以线段AB的中点D的坐标为 ,又直线AB的斜率
,又直线AB的斜率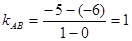 ,因此线段AB的垂直平分线的方程是:
,因此线段AB的垂直平分线的方程是: 即
即 ;
;
从而圆心C的坐标是方程组 的解,解此方程组得C(-3,-2);那么所求圆的半径
的解,解此方程组得C(-3,-2);那么所求圆的半径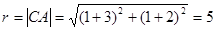 ,故圆心为C的圆的标准方程是:
,故圆心为C的圆的标准方程是: .
.
考点:圆的标准方程

练习册系列答案
相关题目
 与直线
与直线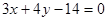 相切于点
相切于点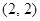 ,其圆心在直线
,其圆心在直线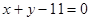 上,求圆
上,求圆 与坐标轴交于点
与坐标轴交于点 .
. 垂直的圆的切线方程;
垂直的圆的切线方程; 是圆上任意一点(不在坐标轴上),直线
是圆上任意一点(不在坐标轴上),直线 交
交 轴于点
轴于点 ,直线
,直线 交直线
交直线 ,
, ,求弦
,求弦 为定值.
为定值.
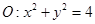 和圆
和圆 .
. 和圆
和圆 的位置关系;
的位置关系; ,求切线
,求切线 交圆
交圆 ,使得圆
,使得圆 ?若存在,求出圆
?若存在,求出圆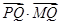 的最小值;
的最小值; 相切的圆的标准方程是
相切的圆的标准方程是 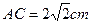 ,过C的割线CMN交
,过C的割线CMN交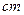 .
.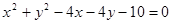 上至少有三个不同点到直线
上至少有三个不同点到直线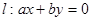 的距离为
的距离为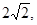 则直线
则直线 的斜率的取值区间为 .
的斜率的取值区间为 .