题目内容
【题目】已知函数f(x)=1-![]() (a>0,a≠1)且f(0)=0.
(a>0,a≠1)且f(0)=0.
(1)求a的值;
(2)若函数g(x)=(2x+1)·f(x)+k有零点,求实数k的取值范围;
(3)当x∈(0,1)时,f(x)>m·2x-2恒成立,求实数m的取值范围.
【答案】(1)a=2(2)(-∞,1)(3)![]()
【解析】
(1)根据![]() ,求得
,求得![]() 的值;(2)由(1)知
的值;(2)由(1)知![]() ,将
,将![]() 的零点转化为函数
的零点转化为函数![]() 与
与![]() 有交点,即可求得
有交点,即可求得![]() 的取值范围;(3)通过参变分离将不等式转化为
的取值范围;(3)通过参变分离将不等式转化为![]() 恒成立,再通过换元转化为求函数的最小值.
恒成立,再通过换元转化为求函数的最小值.
(1)对于函数f(x)=1-![]() (a>0,a≠1),
(a>0,a≠1),
由f(0)=1-![]() =0,得a=2.
=0,得a=2.
(2)由(1)知f(x)=1-![]() =1-
=1-![]() .
.
因为g(x)=(2x+1)·f(x)+k=2x+1-2+k=2x-1+k有零点,
所以函数y=2x的图象和直线y=1-k有交点,所以1-k>0,即k<1.
故实数k的取值范围是(-∞,1).
(3)因为当x∈(0,1)时,f(x)>m·2x-2恒成立,即1-![]() >m·2x-2恒成立,亦即m<
>m·2x-2恒成立,亦即m<![]() -
-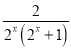 恒成立.
恒成立.
令t=2x,则t∈(1,2),且m<![]() -
-![]() =
=![]() =
=![]() +
+![]() .
.
由于y=![]() +
+![]() 在t∈(1,2)上单调递减,
在t∈(1,2)上单调递减,
所以![]() +
+![]() +
+![]() =
=![]() ,所以m≤
,所以m≤![]() .
.
故实数m的取值范围是![]() .
.

练习册系列答案
相关题目
【题目】假设关于某设备的使用年限![]() (年)和所支出的维修费用
(年)和所支出的维修费用![]() (万元)有如下统计资料:
(万元)有如下统计资料:
| 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
若由资料知, ![]() 对
对![]() 呈线性相关关系,试求:
呈线性相关关系,试求:
(1)回归直线方程;
(2)估计使用年限为10年时,维修费用约是多少?
参考公式:回归直线方程: ![]() .其中
.其中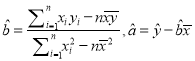
(注: ![]() )
)