题目内容
19.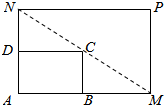 如所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,使点M,N分别在AB,AD的延长线上,且对角线MN过点C,已知AB=2米,AD=3米.
如所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,使点M,N分别在AB,AD的延长线上,且对角线MN过点C,已知AB=2米,AD=3米.(Ⅰ)若要使矩形AMPN的面积不大于32平方米,则DN的长应在什么范围内?
(Ⅱ)当DN的长为多少时,矩形花坛AMPN的面积最小?并求出最小值.
分析 (Ⅰ)设DN的长为x(x>0)米,则AN=(x+3)米,表示出矩形的面积,利用矩形AMPN的面积不大于32平方米,即可求得DN的取值范围.
(Ⅱ)化简矩形的面积,利用基本不等式,即可求得结论.
解答 解:(Ⅰ)设DN的长为x(x>0)米,则AN=(x+3)米
∵$\frac{DN}{AN}=\frac{DC}{AM}$,∴AM=$\frac{2(x+3)}{x}$,
∴矩形AMPN的面积S=AN•AM=$\frac{2(x+3)^{2}}{x}$
∵矩形AMPN的面积不大于32平方米,
∴$\frac{2(x+3)^{2}}{x}$≤32
又x>0得x2-10x+9≤0
解得:1≤x≤9,即DN的长取值范围是[1,9];
(Ⅱ)矩形花坛的面积为S=AN•AM=$\frac{2(x+3)^{2}}{x}$=2x+$\frac{18}{x}$+12≥2$\sqrt{2x•\frac{18}{x}}$+12=24
当且仅当2x=$\frac{18}{x}$,即x=3时,矩形花坛的面积最小为24平方米.
点评 本题考查根据题设关系列出函数关系式,并求出处变量的取值范围;考查利用基本不等式求最值,解题的关键是确定矩形的面积.

练习册系列答案
相关题目
8.已知复数 $z=\frac{1-i}{i}$的共轭复数为( )
| A. | -1-i | B. | 1+i | C. | -1+i | D. | 1-i |
 如图,BD是△ABC外接圆的切线,过A作BD的平行线交BC于E,交△ABC的外接圆于F.
如图,BD是△ABC外接圆的切线,过A作BD的平行线交BC于E,交△ABC的外接圆于F.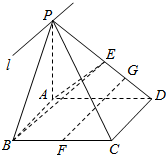 如图,四棱锥P-ABCD,底面ABCD为平行四边形,E、F分别为 PD、BC的中点,面PAB∩面PCD=l.
如图,四棱锥P-ABCD,底面ABCD为平行四边形,E、F分别为 PD、BC的中点,面PAB∩面PCD=l. 如图,已知AB为半圆O的直径,AB=4,C为平面上一点,过点C作半圆的切线CD,过A点作AD⊥CD于D,角半圆于点E,DE=1,则BC的长为( )
如图,已知AB为半圆O的直径,AB=4,C为平面上一点,过点C作半圆的切线CD,过A点作AD⊥CD于D,角半圆于点E,DE=1,则BC的长为( ) 如图,已知AC,BD为圆O的任意两条直径,直线AE,CF是圆O所在平面的两条垂线,且线段AE=CF=$\sqrt{2}$,AC=2.
如图,已知AC,BD为圆O的任意两条直径,直线AE,CF是圆O所在平面的两条垂线,且线段AE=CF=$\sqrt{2}$,AC=2.