题目内容
17．设集合U=R，A={x|2≤x＜4}，B={x|3x-7≥8-2x}．求：A∩B，A∪B，∁U（A∪B），（∁UA）∪B．分析 求出B中不等式的解集确定出B，找出A与B的交集，并集，求出并集的补集，找出A补集与B的并集即可．
解答 解：由B中不等式解得：x≥3，即B={x|x≥3}，
∵A={x|2≤x＜4}，即∁UA={x|x＜2或x≥4}，
∴A∩B={x|3≤x＜4}，A∪B={x|x≥2}，∁U（A∪B）={x|x＜2}，（∁UA）∪B={x|x＜2或x≥3}．
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
5．
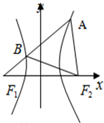如图，F1、F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的左、右焦点，过F1的直线l与双曲线的左右两支分别交于点A、B．若△ABF2为等边三角形，则双曲线的离心率为（ ）
如图，F1、F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的左、右焦点，过F1的直线l与双曲线的左右两支分别交于点A、B．若△ABF2为等边三角形，则双曲线的离心率为（ ）| A． | 4 | B． | $\sqrt{7}$ | C． | $\frac{{2\sqrt{3}}}{3}$ | D． | $\sqrt{3}$ |
9．已知P（2，4）在双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的渐近线上，则该双曲线的离心率为（ ）
| A． | $\sqrt{5}$ | B． | 2 | C． | $\sqrt{3}$ | D． | $\sqrt{2}$ |