题目内容
2.若-$\frac{π}{2}≤x≤\frac{π}{2}$,则函数$y=cosxcos({\frac{π}{2}+x})$的单调递减区间为$[{-\frac{π}{4},\frac{π}{4}}]$.分析 利用倍角公式与正弦函数的单调性即可得出.
解答 解:∵$y=cosxcos({\frac{π}{2}+x})$=-cosxsinx=-$\frac{1}{2}sin2x$,
由2kπ$-\frac{π}{2}$$≤2x≤2kπ+\frac{π}{2}$,解得$kπ-\frac{π}{4}≤x≤kπ+\frac{π}{4}$,k∈Z.
∴$[kπ-\frac{π}{4},kπ+\frac{π}{4}]$∩$[-\frac{π}{2},\frac{π}{2}]$=$[{-\frac{π}{4},\frac{π}{4}}]$,
∴函数$y=cosxcos({\frac{π}{2}+x})$的单调递减区间为$[{-\frac{π}{4},\frac{π}{4}}]$,
故答案为:$[{-\frac{π}{4},\frac{π}{4}}]$.
点评 本题考查了倍角公式与正弦函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
12.设x,y满足约束条件$\left\{\begin{array}{l}{x+y≤4}\\{3x-y≥0}\\{y≥0}\end{array}\right.$,则目标函数z=2x-y的最大值为( )
| A. | -1 | B. | 2 | C. | 4 | D. | 8 |
10.$\int_0^1{(2{x^3}-1)dx}等于$( )
| A. | $-\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 6 |
17.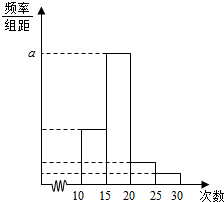 对某校高一年级学生参加“社区志愿者”活动次数进行统计,随机抽取M名学生作为样本,得到这M个学生参加“社区志愿者”活动的次数.据此作出频数和频率统计表及频率分布直方图如下:
对某校高一年级学生参加“社区志愿者”活动次数进行统计,随机抽取M名学生作为样本,得到这M个学生参加“社区志愿者”活动的次数.据此作出频数和频率统计表及频率分布直方图如下:
(Ⅰ)求出表中M,p及图中a的值;
(Ⅱ)若该校高一学生有720人,试估计他们参加“社区志愿者”活动的次数在[15,20)内的人数;
(Ⅲ)若参加“社区志愿者”活动的次数不少于20次的学生可评为“优秀志愿者”,试估计小明被评为“优秀志愿者”的概率.
 对某校高一年级学生参加“社区志愿者”活动次数进行统计,随机抽取M名学生作为样本,得到这M个学生参加“社区志愿者”活动的次数.据此作出频数和频率统计表及频率分布直方图如下:
对某校高一年级学生参加“社区志愿者”活动次数进行统计,随机抽取M名学生作为样本,得到这M个学生参加“社区志愿者”活动的次数.据此作出频数和频率统计表及频率分布直方图如下:| 分组 | 频数 | 频率 |
| [10,15) | 5 | 0.25 |
| [15,20) | 12 | n |
| [20,25) | m | p |
| [25,30] | 1 | 0.05 |
| 合计 | M | 1 |
(Ⅱ)若该校高一学生有720人,试估计他们参加“社区志愿者”活动的次数在[15,20)内的人数;
(Ⅲ)若参加“社区志愿者”活动的次数不少于20次的学生可评为“优秀志愿者”,试估计小明被评为“优秀志愿者”的概率.
7.已知数列{an}满足an=2+1+$\frac{2}{3}$+$\frac{2}{4}$+$\frac{2}{5}$+…+$\frac{2}{{2}^{n}}$,则a101-a100的整数部分为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
14.设集合A={x|x2-9<0},B={x|-1<x≤5},则A∩B=( )
| A. | (-3,-1) | B. | (-3,5] | C. | (3,5] | D. | (-1,3) |
11.已知$a={(\frac{3}{4})^{\frac{1}{3}}}$,$b={log_{\frac{3}{4}}}\frac{1}{3}$,$c={log_3}\frac{3}{4}$,则( )
| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | c>a>b |