题目内容
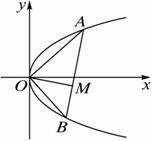
过抛物线y2=4x的顶点O作相互垂直的弦OA、OB,求抛物线顶点O在AB上的影射M的轨迹方程.?
解析:设A(x1,y1)、B(x2,y2),代入抛物线方程并作差得k AB=![]() =
=![]() ,
,
∴直线AB的方程l AB:y-y1=![]() (x-x1).?
(x-x1).?
注意到y12=4x1,y1y2=-16(∵k OA·k OB=-1,?
∴![]() ·
·![]() =-1
=-1![]()
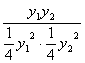 =-1
=-1![]() y1y2=-16),
y1y2=-16),
即得(y1+y2)y+16=4x.
又直线OM的方程为y=-![]() x,?
x,?
由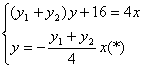
![]() x2+y2-4x=0(x≠0)即为所求的轨迹方程.
x2+y2-4x=0(x≠0)即为所求的轨迹方程.
温馨提示:由(*)消去y1+y2所得方程为所求,是因为由(*)解出x、y(用y1+y2作已知)得到的是点M的坐标,而点M的坐标的关系式(即消去y1+y2得x、y的关系)为动点M的轨迹方程.显然这样做与直接过渡其关系式是一样的.另外本题还可以设OA的斜率为k,类似于上面的方法求M的轨迹方程.

练习册系列答案
相关题目
倾斜角为
的直线过抛物线y2=4x的焦点且与抛物线交于A,B两点,则|AB|=( )
| π |
| 4 |
A、
| ||
B、8
| ||
| C、16 | ||
| D、8 |
过抛物线y2=4x的焦点F的直线交抛物线于A、B两点,点O是坐标原点,若|AF|=5,则△AOB的面积为( )
| A、5 | ||
B、
| ||
C、
| ||
D、
|