题目内容
【题目】已知函数f(x)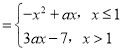 ,若存在x1,x2∈R且x1≠x2,使得f(x1)=f(x2)成立,则实数a的取值范围是( )
,若存在x1,x2∈R且x1≠x2,使得f(x1)=f(x2)成立,则实数a的取值范围是( )
A.[3,+∞)B.(3,+∞)C.(﹣∞,3)D.(﹣∞,3]
【答案】C
【解析】
当![]() 1,即a<2时,由二次函数的图象和性质,可知存在x1,x2∈(﹣∞,1]且x1≠x2,使得f(x1)=f(x2)成立;当
1,即a<2时,由二次函数的图象和性质,可知存在x1,x2∈(﹣∞,1]且x1≠x2,使得f(x1)=f(x2)成立;当![]() 1,即a≥2时,若存在x1,x2∈R且x1≠x2,使得f(x1)=f(x2)成立,则﹣1+a>3a﹣7,由此能求出实数a的取值范围.
1,即a≥2时,若存在x1,x2∈R且x1≠x2,使得f(x1)=f(x2)成立,则﹣1+a>3a﹣7,由此能求出实数a的取值范围.
函数f(x)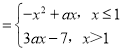 ,
,
存在x1,x2∈R且x1≠x2,使得f(x1)=f(x2)成立,
当![]() 1,即a<2时,由二次函数的图象和性质,可知:
1,即a<2时,由二次函数的图象和性质,可知:
存在x1,x2∈(﹣∞,1]且x1≠x2,使得f(x1)=f(x2)成立,
当![]() 1,即a≥2时,
1,即a≥2时,
若存在x1,x2∈R且x1≠x2,使得f(x1)=f(x2)成立,
则﹣1+a>3a﹣7,
解得a<3,
∴2≤a<3,
综上所述:实数a的取值范围是(﹣∞,3).
故选:C.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目