题目内容

已知函数).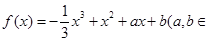

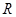(Ⅰ) 若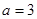，试确定函数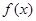的单调区间；

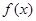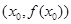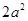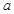(Ⅱ) 若函数在其图象上任意一点处切线的斜率都小于，求实数的取值范围.

 

【答案】

 

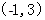 (Ⅰ)单调增区间为，减区间为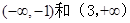

(Ⅱ) 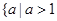或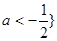

【解析】本试题主要是考查了导数在研究函数中的运用。利用导数符号与函数单调性的关系得到求解，同时考查了导数的几何意义的运用。

（1）由于函数的导函数为二次函数，借助于二次不等式得到增减区间。

（2）利用导数要使得函数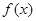在其图象上任意一点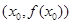处切线的斜率都小于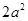，则只要导数恒小于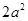即可，转化为恒成立问题来解得。

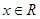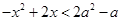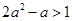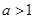因为对任意，恒成立，  所以，解得或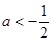，  所以，实数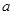的取值范围为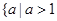或.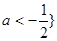 

 

练习册系列答案
相关题目
已知函数f（x）=ax3+bx2-2x+c在x=-2时有极大值6，在x=1时有极小值，
（1）求a，b，c的值；
（2）求f（x）在区间[-3，3]上的最大值和最小值．
已知函数f(x)=2
3
a•sinx•cosx•cos2x-6cos22x+3，且f(
π
24
)=0．
（Ⅰ）求函数f（x）的周期T和单调递增区间；
（Ⅱ）若f（θ）=-3，且θ∈(-
5π
24
，
π
24
)，求θ的值．
已知函数y=asinx+bcosx+c的图象上有一个最低点(
11π
6
，-1)．
（Ⅰ）如果x=0时，y=-
3
2
，求a，b，c．
（Ⅱ）如果将图象上每个点的纵坐标不变，横坐标缩小到原来的
3
π
，然后将所得图象向左平移一个单位得到y=f（x）的图象，并且方程f（x）=3的所有正根依次成为一个公差为3的等差数列，求y=f（x）的解析式．
已知函数f（x）=x2-4，设曲线y=f（x）在点（xn，f（xn））处的切线与x轴的交点为（xn+1，0）（n∈N*），其中x1为正实数．
（Ⅰ）用xn表示xn+1；
（Ⅱ）若x1=4，记an=lg
xn+2xn-2
，证明数列{an}成等比数列，并求数列{xn}的通项公式；
（Ⅲ）若x1=4，bn=xn-2，Tn是数列{bn}的前n项和，证明Tn＜3．
精英家教网已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
π
2
）的部分图象如图所示，则函数f（x）的解析式为（　　）
A、f(x)=2sin(
1
2
x+
π
6
)
B、f(x)=2sin(
1
2
x-
π
6
)
C、f(x)=2sin(2x-
π
6
)
D、f(x)=2sin(2x+
π
6
)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网