题目内容
(.(本小题满分12分)
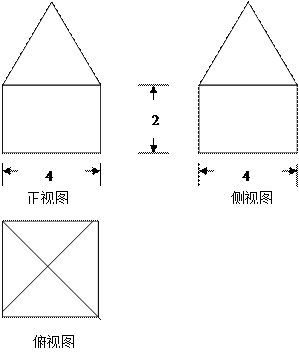
设某几何体及其三视图：如图(尺寸的长度单位：m)
(1)O为AC的中点，证明：BO⊥平面APC；
(2)求该几何体的体积；
(3)求点A到面PBC的距离.
解：(1)证明：由三视图可知，面PAC⊥面ABC，BO⊥AC
∴BO⊥平面APC.(3分)
(2)过P点在面PAC内作PE⊥AC交AC于E，由俯视图可知：CE＝1，AE＝3
又BO＝3，AC＝4，∴S△ABC＝×4×3＝6
∴VP－ABC＝×6×2＝4.(7分)
(3)∵PC＝＝，BE＝＝
∴PB＝＝，BC＝＝
∴cos∠PBC＝＝＝
＝
∴sin∠PBC＝＝
∴S△PBC＝PB·BC·sin∠PBC＝
··
＝
设点A到面PBC的距离为h.
∵VA－PBC＝VP－ABC，∴h·S△PBC＝4
∴h＝
＝＝.(12分)
解析
练习册系列答案
相关题目
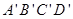如图所示，其中
,
,
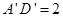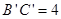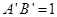，求直角梯形以BC为旋转轴旋转一周形成的几何体的表面积。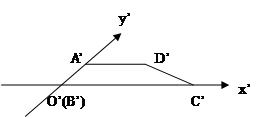
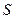平方米塑料片制成圆柱的侧面和下底面（不安装上底面）。
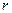取何
值时，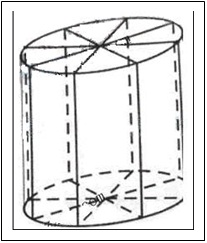
的棱AP、AB上的点，且AD:DP=AE:EB=1:3.求证：DE//平面PBC
一几何体的直观图、主视图、俯视图、左视图．
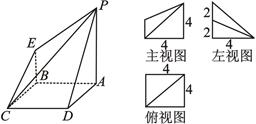
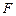为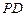
的中点，求证：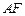
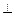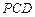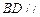面
;
面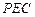
;
底面圆的直径AB的夹角为
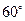，在轴截面中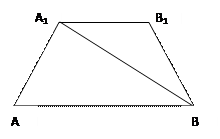
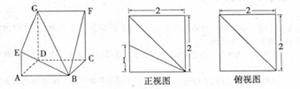
中，平面
平面
，
，
是等边三角形，已知
，
．
（Ⅰ）设
是
上的一点，证明：平面
平面
；
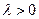使得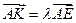
，二面角A—BG—K的大小为
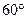，求
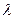的值。