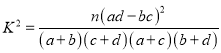题目内容
【题目】某游乐场过山车轨道在同一竖直钢架平面内,如图所示,矩形![]() 的长
的长![]() 为130米,宽
为130米,宽![]() 为120米,圆弧形轨道所在圆的圆心为0,圆O与
为120米,圆弧形轨道所在圆的圆心为0,圆O与![]() ,
,![]() ,
,![]() 分别相切于点A,D,CT为
分别相切于点A,D,CT为![]() 的中点.现欲设计过山车轨道,轨道由五段连接而成:出发点N在线段
的中点.现欲设计过山车轨道,轨道由五段连接而成:出发点N在线段![]() 上(不含端点,游客从点Q处乘升降电梯至点N),轨道第一段
上(不含端点,游客从点Q处乘升降电梯至点N),轨道第一段![]() 与圆O相切于点M,再沿着圆孤轨道
与圆O相切于点M,再沿着圆孤轨道![]() 到达最高点A,然后在点A处沿垂直轨道急速下降至点O处,接着沿直线轨道
到达最高点A,然后在点A处沿垂直轨道急速下降至点O处,接着沿直线轨道![]() 滑行至地面点G处(设计要求M,O,G三点共线),最后通过制动装置减速沿水平轨道
滑行至地面点G处(设计要求M,O,G三点共线),最后通过制动装置减速沿水平轨道![]() 滑行到达终点R记
滑行到达终点R记![]() 为
为![]() ,轨道总长度为l米.
,轨道总长度为l米.
(1)试将l表示为![]() 的函数
的函数![]() ,并写出
,并写出![]() 的取值范围;
的取值范围;
(2)求l最小时![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ,(2)
,(2)![]()
【解析】
(1)作![]() ,垂足为
,垂足为![]() 点,作
点,作![]() ,垂足为
,垂足为![]() 点,可得
点,可得![]() ,
,![]() ,进而得出
,进而得出![]() 以及
以及![]() 的取值范围;
的取值范围;
(2)对![]() 进行求导,求出函数的单调性,即可求得
进行求导,求出函数的单调性,即可求得![]() 最小时
最小时![]() 的值.
的值.
(1)作![]() ,垂足为
,垂足为![]() 点,作
点,作![]() ,垂足为
,垂足为![]() 点,如图所示:
点,如图所示:

∴![]() ,
,![]()
∴![]()
![]() ,
,![]()
(2)![]()
令![]() ,可得
,可得![]() ;令
;令![]() ,可得
,可得![]() .
.
令![]() ,
,![]() ,则当
,则当![]() 时,
时,![]() 为单调递减;当
为单调递减;当![]() 时,
时,![]() 为单调递增.
为单调递增.
∴当![]() 时,函数
时,函数![]() 取得最小值,即
取得最小值,即![]() 最小.
最小.

【题目】2019年电商“双十一”大战即将开始.某电商为了尽快占领市场,抢占今年“双十一”的先机,对成都地区年龄在15到75岁的人群“是否网上购物”的情况进行了调查,随机抽取了100人,其年龄频率分布表和使用网上购物的人数如下所示:(年龄单位:岁)
年龄段 |
|
|
|
|
|
|
频率 | 0.1 | 0.32 | 0.28 | 0.22 | 0.05 | 0.03 |
购物人数 | 8 | 28 | 24 | 12 | 2 | 1 |
(1)若以45岁为分界点,根据以上统计数据填写下面的![]() 列联表,并判断能否在犯错误的概率不超过0.001的前提下认为“网上购物”与年龄有关?
列联表,并判断能否在犯错误的概率不超过0.001的前提下认为“网上购物”与年龄有关?
年龄低于45岁 | 年龄不低于45岁 | 总计 | |
使用网上购物 | |||
不使用网上购物 | |||
总计 |
(2)若从年龄在![]() ,
,![]() 的样本中各随机选取2人进行座谈,记选中的4人中“使用网上购物”的人数为
的样本中各随机选取2人进行座谈,记选中的4人中“使用网上购物”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:
| 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
参考公式: