题目内容
已知函数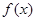 是定义在
是定义在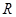 上的单调增函数且为奇函数,数列
上的单调增函数且为奇函数,数列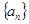 是等差数列,
是等差数列,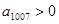 ,则
,则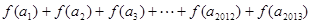 的值( ).
的值( ).
| A.恒为正数 | B.恒为负数 | C.恒为0 | D.可正可负 |
A
解析试题分析:∵函数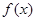 是定义在
是定义在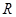 上的奇函数,∴f(0)=0,又函数
上的奇函数,∴f(0)=0,又函数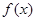 在
在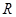 上的单调递增,且数列
上的单调递增,且数列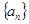 是等差数列,∴
是等差数列,∴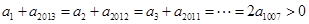 ,∴
,∴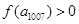 ,∴
,∴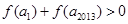 ,
,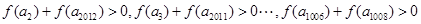 ,∴
,∴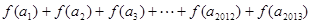 的值恒为正数
的值恒为正数
考点:本题考查了函数的性质及等差数列的性质
点评:利用函数的性质取判断抽象函数值的符号是解决此类问题的关键

练习册系列答案
相关题目
设函数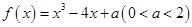 有三个零点
有三个零点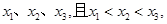 则下列结论正确的是( )
则下列结论正确的是( )
A.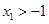 | B.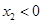 | C.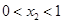 | D.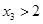 |
函数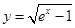 的定义域是( )
的定义域是( )
A.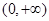 | B.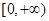 | C.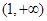 | D. |
设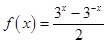 是( )
是( )
| A.奇函数,在(0,+∞)上是减函数 | B.偶函数,在(0,+∞)上是减函数 |
| C.奇函数,在(0,+∞)上是增函数 | D.偶函数,在(0,+∞)上是增函数 |
已知函数 在
在 处取得最大值,则( )
处取得最大值,则( )
A.函数 一定是奇函数 一定是奇函数 | B.函数 一定是偶函数 一定是偶函数 |
C.函数 一定是奇函数 一定是奇函数 | D.函数 一定是偶函数 一定是偶函数 |
已知函数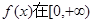 上是减函数,
上是减函数,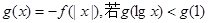 ,则x的取值
,则x的取值
范围是
A.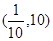 | B.(0,10) | C.(10,+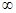 ) ) | D.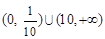 |
已知a=lg3+lg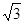 ,b=
,b= lg9,c=lg2,则a,b,c的大小关系是
lg9,c=lg2,则a,b,c的大小关系是
| A.b<a<c | B.c<a<b | C.a<b<c | D.c<b<a |
已知 是奇函数,当
是奇函数,当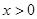 时,
时, 则
则 时,
时, ( )
( )
| A.1 | B.3 | C.-3 | D.-1 |
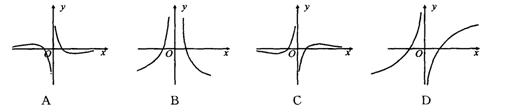
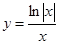 的图象大致是 ( )
的图象大致是 ( )