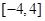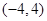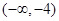题目内容
设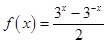 是( )
是( )
| A.奇函数,在(0,+∞)上是减函数 | B.偶函数,在(0,+∞)上是减函数 |
| C.奇函数,在(0,+∞)上是增函数 | D.偶函数,在(0,+∞)上是增函数 |
C
解析试题分析:函数定义域为R,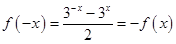 ,所以函数是奇函数,
,所以函数是奇函数,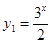 在
在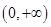 上是增函数,
上是增函数,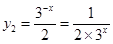 在
在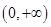 上是减函数,所以
上是减函数,所以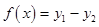 在
在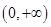 上是增函数
上是增函数
考点:函数性质奇偶性单调性
点评:判断奇偶性先判断定义域是否对称,在看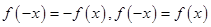 是否成立,从而确定函数是奇函数还是偶函数,如果函数图象易做出,则可作出图像,看图像关于原点对称则为奇函数,关于y轴对称则为偶函数,判断单调性可用定义法,可用导数法,若函数在某区间上导数大于零,则函数在该区间上是增函数,反之则为减函数,通过导数判定函数单调性,求单调区间是高考的必考知识点
是否成立,从而确定函数是奇函数还是偶函数,如果函数图象易做出,则可作出图像,看图像关于原点对称则为奇函数,关于y轴对称则为偶函数,判断单调性可用定义法,可用导数法,若函数在某区间上导数大于零,则函数在该区间上是增函数,反之则为减函数,通过导数判定函数单调性,求单调区间是高考的必考知识点

练习册系列答案
相关题目
已知函数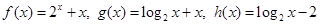 的零点依次为
的零点依次为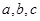 ,则( )
,则( )
A.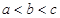 | B.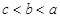 | C.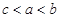 | D.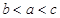 |
若函数 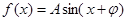 (A>0)在
(A>0)在 处取最大值,则 ( )
处取最大值,则 ( )
A.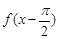 一定是奇函数 一定是奇函数 | B. 一定是偶函数 一定是偶函数 |
C. 一定是奇函数 一定是奇函数 | D. 一定是偶函数 一定是偶函数 |
函数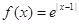 的单调递减区间是( )
的单调递减区间是( )
A.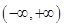 | B.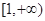 | C. | D.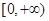 |
函数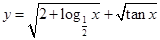 的定义域是( )
的定义域是( )
A. | B.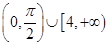 |
C.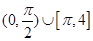 | D.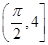 |
已知函数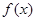 是定义在
是定义在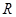 上的单调增函数且为奇函数,数列
上的单调增函数且为奇函数,数列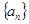 是等差数列,
是等差数列,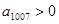 ,则
,则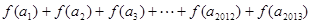 的值( ).
的值( ).
| A.恒为正数 | B.恒为负数 | C.恒为0 | D.可正可负 |
设f(x)为周期是2的奇函数,当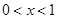 时,f(x)=x(x+1),则当
时,f(x)=x(x+1),则当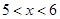 时,f(x)的表达式为
时,f(x)的表达式为
| A.(x-5)(x-4) | B.(x-6)(x-5) | C.(x-6)(5-x) | D.(x-6)(7-x) |
下列函数中,在区间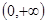 为增函数的是( )
为增函数的是( )
A.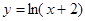 | B.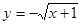 | C. | D.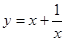 |
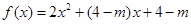 ,
,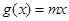 ,若对于任一实数
,若对于任一实数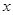 ,
,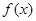 与
与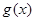 的值至少有一个为正数,则实数
的值至少有一个为正数,则实数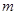 的取值范围是( )
的取值范围是( )