Question

已知数列{a_n}的通项公式a_n＞0(0∈N^*),它的前n项和记为S_n，数列{S_n²}是首项为3，公差为1的等差数列.

(1)求a_n与S_n的解析式；

(2)试比较S_n与3na_n(n∈N^*)的大小.

Answer 1

解析：(1)由已知S_n²=3+(n-1)=n+2.

∵a_n＞0(n∈N^*).∴S_n=(n∈N^*).a₁=S₁=.

当n≥2时，a_n=S_n-S_n-1=.

∴a_n=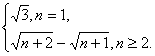

(2)当n=1时，S₁=，3a₁=3,有S₁＜3a₁；

当n=2时，S₂=，3·2a₂=6(-),有S₂＞3·2·a₂；

当n=3时，S₃=，3·3a₃=9(-)，有S₃＞3·3·a₃；

当n=4时，S₄=，3·4a₄=12(-)，有S₄＜3·4·a₄；

当n=5时，S₅=，3·5a₅=15(-)，有S₅＜3·5·a₅.

猜想，当n≥4时，S_n＜3na_n,证明如下：.

∵＞0,

∴只需证明＜3n,

只需证明,

只需证明(n+2)+＜3n.

由平均值定理，有＜=n+,

∴只需证明2n+＜3n.只需证n＞.

此不等式当n≥4时成立，所以S_n＜3na_n，当n≥4时成立.

综上，当n=1或n≥4,n∈N^*时，S_n＜3na_n；

当n=2和n=3时，S_n＞3na_n.

温馨提示

    应该完整的记忆公式a_n=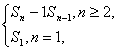容易漏掉n=1的情况.对(2)，直接由条件推导结论比较困难，故用分析法.