题目内容
4.抛物线y2=4x上一点到其焦点距离为3,则该点坐标为(1,±3).分析 根据抛物线的定义可知该点到准线的距离与其到焦点的距离相等,进而利用点到直线的距离求得点的横坐标x的值,代入抛物线方程求得y值,即可得到所求点的坐标.
解答 解:抛物线y2=4x的准线方程为x=-1,
∵抛物线y2=4x上一点到其焦点距离为3,
则该点到抛物线的准线的距离为3,
∴所求点的横坐标为2,代入y2=4x,得$y=±2\sqrt{2}$.
故答案为:(2,±$2\sqrt{2}$).
点评 本题主要考查了抛物线的简单性质.在涉及焦点弦和关于焦点的问题时常用抛物线的定义来解决,是中档题.

练习册系列答案
相关题目
16.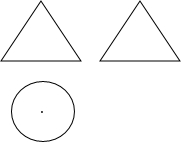 图中的三视图表示的几何体为( )
图中的三视图表示的几何体为( )
 图中的三视图表示的几何体为( )
图中的三视图表示的几何体为( )| A. | 圆柱 | B. | 圆锥 | C. | 圆台 | D. | 三棱柱 |
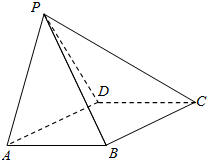 如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠DAB=60°,AB=2,△PAD为等边三角形,平面PAD⊥平面ABCD.
如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠DAB=60°,AB=2,△PAD为等边三角形,平面PAD⊥平面ABCD.