Question

【题目】已知椭圆： 的离心率为，直线交椭圆于、两点，椭圆的右顶点为，且满足.

（1）求椭圆的方程；

（2）若直线与椭圆交于不同两点、，且定点满足，求实数的取值范围.

Answer 1

【答案】（1）.

（2）.

【解析】试题分析：

（1）根据可求得，再由离心率可得c，于是可求得b，进而得到椭圆的方程．（2）结合直线和椭圆的位置关系求解．将直线方程和椭圆方程联立消元后得到二次方程，由判别式大于零可得，结合可得，从而得到关于的不等式组，解不等式组可得所求范围．

试题解析：

（1）∵，

∴，

又，

∴，

∴，

∴椭圆的方程为.

（2）由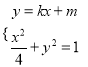消去y整理得： ，

∵直线与椭圆交于不同的两点、，

∴，

整理得．

设， ，

则，

又设中点的坐标为，

∴， ．

∵，

∴，即，

∴，

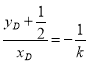∴，解得．

∴实数的取值范围．