题目内容
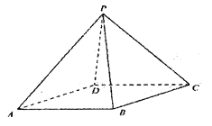
【题目】如图,四棱锥![]() 的底面是正方形,每条侧棱的长都是底面边长的
的底面是正方形,每条侧棱的长都是底面边长的![]() 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.
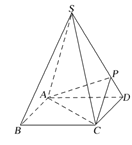
(1)求证:![]() ;
;
(2)若![]() 平面PAC,则侧棱SC上是否存在一点E,使得BE∥平面PAC?若存在,求SE:EC;若不存在,试说明理由.
平面PAC,则侧棱SC上是否存在一点E,使得BE∥平面PAC?若存在,求SE:EC;若不存在,试说明理由.
【答案】(1)证明见解析;(2)存在,2:1
【解析】
(1)先证明AC⊥面SBD,然后利用线面垂直的性质证明AC⊥SD;
(2)利用线面平行的性质定理确定E的位置,然后求出SE:EC的值.
(1)证明:连BD,设AC交BD于O,由题意SO⊥AC,
在正方形ABCD中,AC⊥BD,
所以AC⊥面SBD,
所以AC⊥SD.
(2)解:若SD⊥平面PAC,
则SD⊥OP,
设正方形ABCD的边长为a,
则SD![]() ,OD
,OD![]() ,
,
则OD2=PDSD,
可得PD![]() ,
,
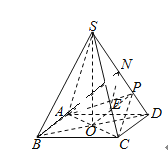
故可在SP上取一点N,使PN=PD,
过N作PC的平行线与SC的交点即为E,连BN.
在△BDN中知BN∥PO,
又由于NE∥PC,故平面BEN∥面PAC,
得BE∥面PAC,
由于SN:NP=2:1,
故SE:EC=2:1.

练习册系列答案
相关题目
【题目】[2019·清远期末]一只红铃虫的产卵数![]() 和温度
和温度![]() 有关,现收集了4组观测数据列于下表中,根据数据作出散点图如下:
有关,现收集了4组观测数据列于下表中,根据数据作出散点图如下:
温度 | 20 | 25 | 30 | 35 |
产卵数 | 5 | 20 | 100 | 325 |

(1)根据散点图判断![]() 与
与![]() 哪一个更适宜作为产卵数
哪一个更适宜作为产卵数![]() 关于温度
关于温度![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程(数字保留2位小数);
的回归方程(数字保留2位小数);
(3)要使得产卵数不超过50,则温度控制在多少![]() 以下?(最后结果保留到整数)
以下?(最后结果保留到整数)
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
| 5 | 20 | 100 | 325 |
| 1.61 | 3 | 4.61 | 5.78 |