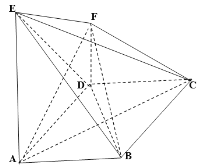
题目内容
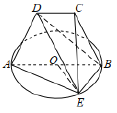
【题目】菱形![]() 中,
中,![]()
![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,
(1)证明:直线![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)线段![]() 上是否存在点
上是否存在点![]() 使得直线
使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ?若存在,求
?若存在,求![]() ;若不存在,说明理由.
;若不存在,说明理由.
【答案】(1)证明见解析(2)![]() (3)存在,
(3)存在,![]()
【解析】
(1)建立以![]() 为原点,分别以
为原点,分别以![]() ,
,![]() (
(![]() 为
为![]() 中点),
中点),![]() 的方向为
的方向为![]() 轴,
轴,![]() 轴,
轴,![]() 轴正方向的空间直角坐标系,求出直线
轴正方向的空间直角坐标系,求出直线![]() 的方向向量,平面
的方向向量,平面![]() 的法向量,证明向量垂直,得到线面平行;
的法向量,证明向量垂直,得到线面平行;
(2)利用空间向量法求出二面角的余弦值,再由同角三角函数的基本关系求出正弦值;
(3)设![]() ,则
,则![]() ,利用空间向量求表示出线面角的正弦值,求出
,利用空间向量求表示出线面角的正弦值,求出![]() 的值,得解.
的值,得解.
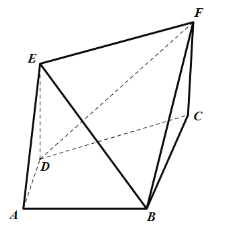
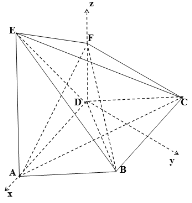
解:建立以![]() 为原点,分别以
为原点,分别以![]() ,
,![]() (
(![]() 为
为![]() 中点),
中点),![]() 的方向为
的方向为![]() 轴,
轴,![]() 轴,
轴,![]() 轴正方向的空间直角坐标系(如图),
轴正方向的空间直角坐标系(如图),
则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
(1)证明:![]() ,
,![]() ,
,
设![]() 为平面
为平面![]() 的法向量,
的法向量,
则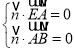 ,即
,即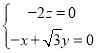 ,
,
可得![]() ,
,
又![]() ,可得
,可得![]() ,
,
又因为直线![]() 平面
平面![]() ,所以直线
,所以直线![]() 平面
平面![]() ;
;
(2)![]() ,
,![]() ,
,![]() ,
,
设![]() 为平面
为平面![]() 的法向量,
的法向量,
则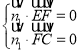 ,即
,即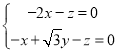 ,可得
,可得![]() ,
,
设![]() 为平面
为平面![]() 的法向量,
的法向量,
则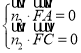 ,即
,即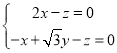 ,可得
,可得![]() ,
,
所以 ,
,
![]()
所以二面角![]() 的正弦值为
的正弦值为![]() ;
;
(3)设![]() ,则
,则![]() ,
,
则![]() ,
,![]() ,
,
设![]() 为平面
为平面![]() 的法向量,
的法向量,
则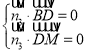 ,即
,即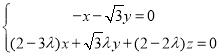 ,
,
可得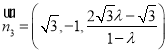 ,
,
由![]() ,得
,得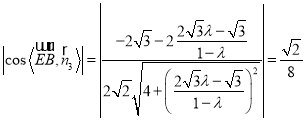 ,
,
解得![]() 或
或![]() (舍),所以
(舍),所以![]() .
.

【题目】今年,新型冠状病毒来势凶猛,老百姓一时间“谈毒色变”,近来,有关喝白酒可以预防病毒的说法一直在民间流传,更有人拿出“医”字的繁体字“醫”进行解读为:医治瘟疫要喝酒,为了调查喝白酒是否有助于预防病毒,我们调查了1000人的喝酒生活习惯与最终是否得病进行了统计,表格如下:
每周喝酒量(两) |
|
|
|
|
|
人数 | 100 | 300 | 450 | 100 |
|
规定:①每周喝酒量达到4两的叫常喝酒人,反之叫不常喝酒人;
②每周喝酒量达到8两的叫有酒瘾的人.
(1)求![]() 值,从每周喝酒量达到6两的人中按照分层抽样选出6人,再从这6人中选出2人,求这2人中无有酒瘾的人的概率;
值,从每周喝酒量达到6两的人中按照分层抽样选出6人,再从这6人中选出2人,求这2人中无有酒瘾的人的概率;
(2)请通过上述表格中的统计数据,填写完下面的![]() 列联表,并通过计算判断是否能在犯错误的概率不超过0.1的前提下认为是否得病与是否常喝酒有关?并对民间流传的说法做出你的判断.
列联表,并通过计算判断是否能在犯错误的概率不超过0.1的前提下认为是否得病与是否常喝酒有关?并对民间流传的说法做出你的判断.
常喝酒 | 不常喝酒 | 合计 | |
得病 | |||
不得病 | 250 | 650 | |
合计 |
参考公式: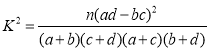 ,其中
,其中![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |