题目内容
【题目】在直角坐标系
中，曲线
的参数方程为
(其中
为参数)，曲线
.以原点
为极点，
轴的正半轴为极轴建立极坐标系.
(1)求曲线、
的极坐标方程；
(2)射线
与曲线、分别交于点
(且均异于原点)当
时，求
的最小值.
【答案】(1)
的极坐标方程为
，
的极坐标方程为
；(2)
.
【解析】【试题分析】(1)利用
消去参数得到圆的直角坐标方程,在转化为极坐标方程,直接利用公式将的直角坐标方程转化为极坐标方程.(2)联立射线和圆的极坐标方程,求得
,联立射线的方程和椭圆的极坐标方程求得
,再用基本不等式求得最小值.
【试题解析】
（1）曲线
的普通方程为
，的极坐标方程为
的极坐标方程为
（2）联立
与的极坐标方程得
，
联立与的极坐标方程得
，
则
= 
=
=
（当且仅当
时取等号）.
的最小值为
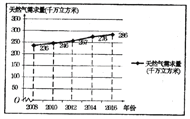
【题目】2017年12月，针对国内天然气供应紧张的问题，某市政府及时安排部署，加气站采取了紧急限气措施，全市居民打响了节约能源的攻坚战.某研究人员为了了解天然气的需求状况，对该地区某些年份天然气需求量进行了统计，并绘制了相应的折线图.
（Ⅰ）由折线图可以看出，可用线性回归模型拟合年度天然气需示量
(单位：千万立方米)与年份
(单位：年)之间的关系.并且已知关于的线性回归方程是
，试确定
的值，并预测2018年该地区的天然气需求量；
（Ⅱ）政府部门为节约能源出台了《购置新能源汽车补贴方案》，该方案对新能源汽车的续航里程做出了严格规定，根据续航里程的不同，将补贴金额划分为三类，A类：每车补贴1万元，B类：每车补贴2.5万元，C类：每车补贴3.4万元.某出租车公司对该公司60辆新能源汽车的补贴情况进行了统计，结果如下表：
类型 |
|
|
|
车辆数目 | 10 | 20 | 30 |
为了制定更合理的补贴方案，政府部门决定利用分层抽样的方式了解出租车公司新能源汽车的补贴情况，在该出租车公司的60辆车中抽取6辆车作为样本，再从6辆车中抽取2辆车进一步跟踪调查.若抽取的2辆车享受的补贴金额之和记为“
”，求的分布列及期望.
【题目】已知某班的50名学生进行不记名问卷调查，内容为本周使用手机的时间长，如表：
时间长（小时） |
|
|
|
|
|
女生人数 | 4 | 11 | 3 | 2 | 0 |
男生人数 | 3 | 17 | 6 | 3 | 1 |
（1）求这50名学生本周使用手机的平均时间长；
（2）时间长为
的7名同学中，从中抽取两名，求其中恰有一个女生的概率；
（3）若时间长为
被认定“不依赖手机”，
被认定“依赖手机”，根据以上数据完成
列联表：
不依赖手机 | 依赖手机 | 总计 | |
女生 | |||
男生 | |||
总计 |
能否在犯错概率不超过0.15的前提下，认为学生的性别与依赖手机有关系？
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（参考公式：
，
）
【题目】某石化集团获得了某地深海油田区块的开采权．集团在该地区随机初步勘探了部分几口井．取得了地质资料，进入全面勘探时期后．集团按网络点来布置井位进行全面勘探．由于勘探一口井的费用很高．如果新设计的井位与原有井位重合或接近．便利用旧并的地质资料．不必打这日新并，以节约勘探费与用，勘探初期数据资料见如表：
井号 |
|
|
|
|
|
|
坐标 |
|
|
|
|
|
|
钻探深度 |
|
|
|
|
|
|
出油量 |
|
|
|
|
|
|
（参考公式和计算结果：
，
，
，
）．
（
）
号旧井位置线性分布，借助前
组数据求得回归直线方程为
，求
的值．
（
）现准备勘探新井
，若通过，
，，
号井计算出的
，
的值（，精确到
）相比于（）中的
，
，值之差不超过
．则使用位置最接近的已有旧井
．否则在新位置打开，请判断可否使用旧井？
（）设出油量与勘探深度的比值
不低于
的勘探井称为优质井，那么在原有
口井中任意勘探
口井，求勘探优质井数
的分布列与数学期望．
