Question

【题目】一张坐标纸上涂着圆E： 及点P（1，0），折叠此纸片，使P与圆周上某点P'重合，每次折叠都会留下折痕，设折痕与直线EP'交于点M．

（1）求的轨迹的方程；

（2）直线与C的两个不同交点为A，B，且l与以EP为直径的圆相切，若，求△ABO的面积的取值范围．

Answer 1

【答案】（1）；（2）.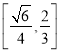

【解析】试题分析： 折痕为的垂直平分线，则，推导出的轨迹是以， 为焦点的椭圆，且,由此能求出的轨迹的方程；

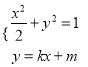与为直径的圆相切，从而，由，得

，由此利用根的判别式，韦达定理，向量的数量积，弦长公式，三角形面积公式，能求出的面积的取值范围。

解析：（1）折痕为PP′的垂直平分线，则|MP|=|MP′|，由题意知圆E的半径为2，

∴|ME|+|MP|=|ME|+|MP′|=2＞|EP|，

∴E的轨迹是以E、P为焦点的椭圆，且a=，c=1，

∴b2=a2﹣c2=1， ∴M的轨迹C的方程为．

（2）l与以EP为直径的圆x2+y2=1相切，

则O到l即直线AB的距离：=1，即m2=k2+1，

由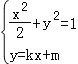，消去y，得（1+2k2）x2+4kmx+2m2﹣2=0，

∵直线l与椭圆交于两个不同点，

∴△=16k2m2﹣8（1+2k2）（m2﹣1）=8k2＞0，k2＞0，

设A（x1，y1），B（x2，y2），则，，

y1y2=（kx1+m）（kx2+m）=k2x1x2+km（x1+x2）+m2=，

又=x1x2+y1y2=，∴，∴，

==，

设μ=k4+k2，则，∴=，，

∵S△AOB关于μ在[，2]单调递增，

∴，∴△AOB的面积的取值范围是[，]．