题目内容
【题目】已知U=R且A={x|a2x2-5ax-6<0},B{x||x-2|≥1}.
(1)若a=1,求(UA)![]() B;
B;
(2)求不等式a2x2-5ax-6<0(a∈R)的解集.
【答案】(1){x|x≤-1或x≥6};(2)a=0时,不等式的解集为R;a>0时,不等式的解集为(-![]() ,
,![]() );a<0时,不等式的解集为(
);a<0时,不等式的解集为(![]() ,-
,-![]() ).
).
【解析】
(1)解不等式求出集合![]() ,
,![]() ,再由集合运算法则计算.
,再由集合运算法则计算.
(2)分类讨论,![]() ,
,![]() 时,方程
时,方程![]() 两根为
两根为![]() 和
和![]() ,按它们的大小分类得解集.
,按它们的大小分类得解集.
(1)a=1时,A={x|x2-5x-6<0}={x|-1<x<6},B={x||x-2|≥1}={x|x≤1或x≥3};
∴UA={x|x≤-1或x≥6},
则(UA)![]() B={x|x≤-1或x≥6};
B={x|x≤-1或x≥6};
(2)a=0时,不等式化为-6<0,解集为R;
当a≠0时,不等式化为(ax+1)(ax-6)<0,即(x+![]() )(x-
)(x-![]() )<0;
)<0;
若a>0,则-![]() <
<![]() ,不等式的解集为(-
,不等式的解集为(-![]() ,
,![]() );
);
若a<0,则-![]() >
>![]() ,不等式的解集为(
,不等式的解集为(![]() ,-
,-![]() );
);
综上知,a=0时,不等式的解集为R;
a>0时,不等式的解集为(-![]() ,
,![]() );
);
a<0时,不等式的解集为(![]() ,-
,-![]() ).
).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
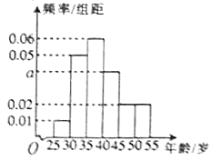
【题目】某电子商务平台的管理员随机抽取了1000位上网购物者,并对其年龄(在10岁到69岁之间)进行了调查,统计情况如下表所示.
年龄 |
|
|
|
|
|
|
人数 | 100 | 150 |
| 200 |
| 50 |
已知![]() ,
,![]() ,
,![]() 三个年龄段的上网购物的人数依次构成递减的等比数列.
三个年龄段的上网购物的人数依次构成递减的等比数列.
(1)求![]() 的值;
的值;
(2)若将年龄在![]() 内的上网购物者定义为“消费主力军”,其他年龄段内的上网购物者定义为“消费潜力军”.现采用分层抽样的方式从参与调查的1000位上网购物者中抽取5人,再从这5人中抽取2人,求这2人中至少有一人是消费潜力军的概率.
内的上网购物者定义为“消费主力军”,其他年龄段内的上网购物者定义为“消费潜力军”.现采用分层抽样的方式从参与调查的1000位上网购物者中抽取5人,再从这5人中抽取2人,求这2人中至少有一人是消费潜力军的概率.