题目内容

17．M（x0，y0）为圆x2+y2=a2（a＞0）内异于圆心的一点，则直线x•x0+y•y0=a2与该圆的位置关系为（　　）
A．相离B．相交C．相切D．相切或相离

分析 由题意可得：x02+y02＜a2，解得圆心到直线的距离d=$\frac{{a}^{2}}{\sqrt{{x}_{0}^{2}{+y}_{0}^{2}}}$＞a，即可得解．

解答 解：∵点M在圆内，
∴故x02+y02＜a2，
∴圆心到直线的距离d=$\frac{{a}^{2}}{\sqrt{{x}_{0}^{2}{+y}_{0}^{2}}}$＞a．
故直线与圆相离．
故选：A．

点评 本题主要考查了点到直线的距离公式的应用，考查了点与圆的位置关系，属于基本知识的考查．

练习册系列答案
相关题目
7．已知函数f（x）=$\sqrt{3}$sinxcosx-cos2x+1
（1）求函数f（x）的单调递增区间；
（2）若f（$\frac{θ}{2}$+$\frac{π}{12}$）=$\frac{5}{6}$，θ∈（0，$\frac{π}{2}$），求cos（θ+$\frac{π}{4}$）的值．
8．在（1+x）n的展开式中，第9项为（　　）
A．C${\;}_{n}^{9}$x9B．C${\;}_{n}^{8}$x8C．C${\;}_{n}^{9}$xn-9D．C${\;}_{n}^{8}$xn-8
5．某校卫生所成立了调查小组，调查“按时刷牙与患龋齿的关系”，对该校某年级700 名学生进行检查，按患龋齿和不患龋齿分类，得汇总数据：按时刷牙且不患龋齿的学生有60 名，不按时刷牙但不患龋齿的学生有100 名，按时刷牙但患龋齿的学生有 140 名．
（1）能否在犯错概率不超过 0.01 的前提下，认为该年级学生的按时刷牙与患龋齿有关系？
（2）4名校卫生所工作人员甲、乙、丙、丁被随机分成两组，每组 2 人，一组负责数据收集，
另一组负责数据处理，求工作人员甲分到“负责收集数据组”并且工作人员乙分到“负责数据处理组”的概率
P（K2≥k0）0.0100.0050.001
k06.6357.87910.828
附：k2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．
12．我国对PM2.5采用如下标准：
PM2.5日均值m（微克/立方米）空气质量等级
m＜35一级
35≤m≤75二级
m＞75超标
某地4月1日至15日每天的PM2.5监测数据如茎叶图所示．
（Ⅰ）期间刘先生有两天经过此地，这两天此地PM2.5监测数据均未超标．请计算出这两天空气质量恰好有一天为一级的概率；
（Ⅱ）从所给15天的数据中任意抽取三天数据，记ξ表示抽到PM2.5监测数据超标的天数，求ξ的分布列及期望．
2．已知函数$f（x）=\frac{2x+3}{3x}$，数列{an}满足a1=1，${a_{n+1}}=f（\frac{1}{a_n}），（n∈{N^*}）$，
（1）求数列{an}的通项公式；
（2）设${b_n}=\frac{1}{{{a_{n-1}}{a_n}}}（n≥2）$，b1=3，Sn=b1+b2+…+bn，若${S_n}＜\frac{m-2002}{2}$对一切n∈N*成立，求最小正整数m的值．
9．已知某运动员每次投篮命中的概率都为40%．现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率：先由计算器算出0到9之间取整数值的随机数，用1，2，3，4表示命中，用5，6，7，8，9，0表示不命中；再以每三个随机数为一组，代表三次投篮的结果．经随机模拟产生了20组随机数：
907    966    191     925     271    932    812    458     569   683
431    257    393     027     556    488    730    113     537   989
据此估计，该运动员三次投篮恰有两次命中的概率为（　　）
A．0.35B．0.30C．0.25D．0.20
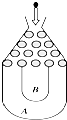6．将一个半径适当的小球放入如图所示的容器最上方的入口处，小球自由下落，小球在下落的过程中，将遇到黑色障碍物3次，最后落入A袋或B袋中．已知小球每次遇到障碍物时，向左、右两边下落的概率分别是p，1-p．
（Ⅰ）当p为何值时，小球落入B袋中的概率最大，并求出最大值；
（Ⅱ）在容器的入口处依次放入4个小球，记ξ为落入B袋中的小球个数，当p=$\frac{1}{3}$时，求ξ的数学期望．
7．已知数列{an}，{bn}满足：a1b1+a2b2+a3b3+…+anbn=（n-1）•2n+1+2（n∈N*），若{bn}是首项为1，公比为2的等比数列，则数列{an}的通项公式是（　　）
A．an=2n-1B．an=2nC．an=2nD．an=2n-1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网