题目内容
13.计算:(1)${(2\frac{3}{5})^0}+{2^{-4}}×{(2\frac{1}{4})^{-\frac{3}{2}}}-{0.01^{0.5}}$;
(2)(lg2)2+lg2•lg50+lg25.
分析 (1)利用有理指数幂的运算法则求解即可.
(2)利用对数运算法则化简求解即可.
解答 (本小题满分17分)
解:(1)原式=$1+\frac{1}{16}×{[{{{(\frac{3}{2})}^2}}]^{-\;\frac{3}{2}}}-{({10^{-2}})^{\frac{1}{2}}}$…(5分)
=$1+\frac{1}{16}×\frac{8}{27}-\frac{1}{10}=\frac{124}{135}$…(9分)
(2)原式=lg2(lg2+lg50)+lg25…(13分)
=2lg2+lg25=2…(17分)
点评 本题考查对数运算法则以及有理指数幂的运算法则的应用,考查计算能力.

练习册系列答案
相关题目
4.已知具有线性相关的两个变量x,y之间的一组数据如表:
且回归方程是$\widehat{y}$=0.95x+2.6,则t=( )
| x | 0 | 1 | 2 | 3 | 4 |
| y | 2.2 | 4.3 | t | 4.8 | 6.7 |
| A. | 4.7 | B. | 4.6 | C. | 4.5 | D. | 4.4 |
1.已知集合∁RM={x|lnx<e},$N=\{y|y=\frac{1}{x}(x>0)\}$,则M∩N=( )
| A. | (0,e) | B. | [e,ee) | C. | [ee,+∞) | D. | (e,+∞) |
8. 阅读程序框图,若输出的$y=\frac{1}{2}$,则输入的x的值可能为( )
阅读程序框图,若输出的$y=\frac{1}{2}$,则输入的x的值可能为( )
 阅读程序框图,若输出的$y=\frac{1}{2}$,则输入的x的值可能为( )
阅读程序框图,若输出的$y=\frac{1}{2}$,则输入的x的值可能为( )| A. | -1 | B. | 0 | C. | 5 | D. | 1 |
2.若高次不等式(-x3+x2+2x)(x2-1)≥0,则x的取值范围为( )
| A. | (-∞,0) | B. | (-∞,0] | C. | (-∞,0]∪[1,2] | D. | [1,2] |
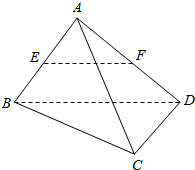 在空间四边形ABCD中,E,F分别是AB,AD的中点
在空间四边形ABCD中,E,F分别是AB,AD的中点