题目内容
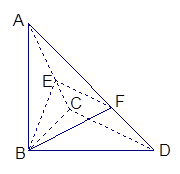
如图,四边形ABEF和ABCD都是直角梯形,∠BAD=∠FAB=90°,BC∥= AD,BE∥=
AD,BE∥= FA,G、H分别为FA、FD的中点.
FA,G、H分别为FA、FD的中点.

(1)证明:四边形BCHG是平行四边形.
(2)C、D、F、E四点是否共面?为什么?
 AD,BE∥=
AD,BE∥= FA,G、H分别为FA、FD的中点.
FA,G、H分别为FA、FD的中点.
(1)证明:四边形BCHG是平行四边形.
(2)C、D、F、E四点是否共面?为什么?
(1)见解析(2)四点共面
(1)证明:由已知FG=GA,FH=HD,可得GH∥= AD.又BC∥=
AD.又BC∥= AD,∴GH∥=BC.∴四边形BCHG为平行四边形.
AD,∴GH∥=BC.∴四边形BCHG为平行四边形.
(2)解:(解法1)由BE∥= AF,G为FA中点知,BE∥=FG,∴四边形BEFG为平行四边形.∴EF∥BG.由(1)知BG∥CH,∴EF∥CH,∴EF与CH共面.又D∈FH,∴C、D、F、E四点共面.
AF,G为FA中点知,BE∥=FG,∴四边形BEFG为平行四边形.∴EF∥BG.由(1)知BG∥CH,∴EF∥CH,∴EF与CH共面.又D∈FH,∴C、D、F、E四点共面.
(解法2)如图,延长FE、DC分别与AB交于点M、M′,∵BE∥= AF,∴B为MA中点.
AF,∴B为MA中点.

∵BC∥= AD,∴B为M′A中点.∴M与M′重合,即FE与DC交于点M(M′).∴C、D、F、E四点共面
AD,∴B为M′A中点.∴M与M′重合,即FE与DC交于点M(M′).∴C、D、F、E四点共面
 AD.又BC∥=
AD.又BC∥= AD,∴GH∥=BC.∴四边形BCHG为平行四边形.
AD,∴GH∥=BC.∴四边形BCHG为平行四边形.(2)解:(解法1)由BE∥=
 AF,G为FA中点知,BE∥=FG,∴四边形BEFG为平行四边形.∴EF∥BG.由(1)知BG∥CH,∴EF∥CH,∴EF与CH共面.又D∈FH,∴C、D、F、E四点共面.
AF,G为FA中点知,BE∥=FG,∴四边形BEFG为平行四边形.∴EF∥BG.由(1)知BG∥CH,∴EF∥CH,∴EF与CH共面.又D∈FH,∴C、D、F、E四点共面.(解法2)如图,延长FE、DC分别与AB交于点M、M′,∵BE∥=
 AF,∴B为MA中点.
AF,∴B为MA中点.
∵BC∥=
 AD,∴B为M′A中点.∴M与M′重合,即FE与DC交于点M(M′).∴C、D、F、E四点共面
AD,∴B为M′A中点.∴M与M′重合,即FE与DC交于点M(M′).∴C、D、F、E四点共面
练习册系列答案
相关题目
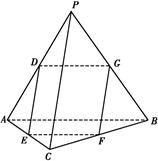
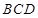 中,
中,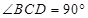 ,
, ,
,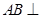 平面
平面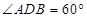 ,
,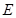 、
、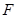 分别是
分别是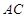 、
、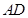 上的动点,且
上的动点,且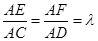
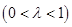 .
.
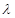 为何值,总有平面
为何值,总有平面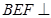 平面
平面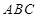 ;
; ?
? 
 α
α PQ
PQ α”改成文字叙述是________.
α”改成文字叙述是________.