题目内容
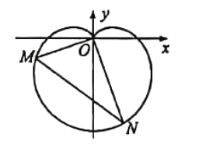
【题目】已知函数![]() (
(![]() R).
R).
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若对任意实数![]() ,当
,当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() ;(Ⅱ)
;(Ⅱ)![]()
【解析】
试题(1)求函数的单调区间,实质上就是解不等式![]() 得增区间,解不等式
得增区间,解不等式![]() 得减区间;(2)函数的最大值一般与函数的单调性联系在一起,本题中
得减区间;(2)函数的最大值一般与函数的单调性联系在一起,本题中![]() ,其单调性要对
,其单调性要对![]() 进行分类,
进行分类,![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,不合题意,故有
上单调递减,不合题意,故有![]() ,按极值点
,按极值点![]() 与0的大小分类研究单调性有最大值.
与0的大小分类研究单调性有最大值.
试题解析:(1)当![]() 时,
时,![]() ,
,
则![]() ,
,
令![]() ,得
,得![]() 或
或![]() ;令
;令![]() ,得
,得![]() ,
,
∴函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)由题意![]() ,
,
(1)当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,此时,不存在实
上单调递减,此时,不存在实
数![]() ,使得当
,使得当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() .
.
(2)当![]() 时,令
时,令![]() ,有
,有![]() ,
,![]() ,
,
①当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,显然符合题意.
上单调递增,显然符合题意.
②当![]() 即
即![]() 时,函数
时,函数![]() 在
在![]() 和
和![]() 上单调递增,
上单调递增,
在![]() 上单调递减,
上单调递减,![]() 在
在![]() 处取得极大值,且
处取得极大值,且![]() ,
,
要使对任意实数![]() ,当
,当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() ,
,
只需![]() ,解得
,解得![]() ,又
,又![]() ,
,
所以此时实数![]() 的取值范围是
的取值范围是![]() .
.
③当![]() 即
即![]() 时,函数
时,函数![]() 在
在![]() 和
和![]() 上单调递增,
上单调递增,
在![]() 上单调递减,要存在实数
上单调递减,要存在实数![]() ,使得当
,使得当![]() 时,
时,
函数![]() 的最大值为
的最大值为![]() ,需
,需![]() ,
,
代入化简得![]() ,①
,①
令![]() ,因为
,因为![]() 恒成立,
恒成立,
故恒有![]() ,所以
,所以![]() 时,①式恒成立,
时,①式恒成立,
综上,实数![]() 的取值范围是
的取值范围是![]() .
.

【题目】某校为举办甲、乙两项不同活动,分别设计了相应的活动方案:方案一、方案二.为了解该校学生对活动方案是否支持,对学生进行简单随机抽样,获得数据如下表:
男生 | 女生 | |||
支持 | 不支持 | 支持 | 不支持 | |
方案一 | 200人 | 400人 | 300人 | 100人 |
方案二 | 350人 | 250人 | 150人 | 250人 |
假设所有学生对活动方案是否支持相互独立.
(Ⅰ)分别估计该校男生支持方案一的概率、该校女生支持方案一的概率;
(Ⅱ)从该校全体男生中随机抽取2人,全体女生中随机抽取1人,估计这3人中恰有2人支持方案一的概率;
(Ⅲ)将该校学生支持方案的概率估计值记为![]() ,假设该校一年级有500名男生和300名女生,除一年级外其他年级学生支持方案二的概率估计值记为
,假设该校一年级有500名男生和300名女生,除一年级外其他年级学生支持方案二的概率估计值记为![]() ,试比较
,试比较![]() 与
与![]() 的大小.(结论不要求证明)
的大小.(结论不要求证明)