题目内容
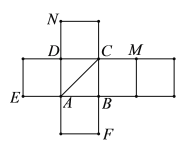
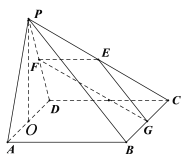
【题目】如图,在边长为4的正三角形![]() 中,E为边
中,E为边![]() 的中点,过E作
的中点,过E作![]() 于D.把
于D.把![]() 沿
沿![]() 翻折至
翻折至![]() 的位置,连结
的位置,连结![]() .翻折过程中,其中正确的结论是( )
.翻折过程中,其中正确的结论是( )
A.![]() ;
;
B.存在某个位置,使![]() ;
;
C.若![]() ,则
,则![]() 的长是定值;
的长是定值;
D.若![]() ,则四面体
,则四面体![]() 的体积最大值为
的体积最大值为![]()
【答案】ACD
【解析】
根据线面垂直的性质判断A,B;取![]() 中点
中点![]() ,可证明
,可证明![]() ,从而可计算出
,从而可计算出![]() ,判断C;折叠过程中,
,判断C;折叠过程中,![]() 不动,当
不动,当![]() 到平面
到平面![]() 的距离最大时,四面体
的距离最大时,四面体![]() 的体积最大,从而计算出最大体积后判断D.
的体积最大,从而计算出最大体积后判断D.
由![]() ,
,![]() ,
,![]() 得
得![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() ,A正确;
,A正确;
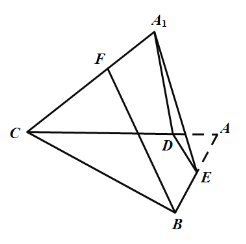
若存在某个位置,使![]() ,如图,连接
,如图,连接![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
连接![]() ,正
,正![]() 中,
中,![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,所以
,所以![]() ,由选项A的判断有
,由选项A的判断有![]() ,且
,且![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() ,则
,则![]() ,这是不可能的,事实上
,这是不可能的,事实上![]() ,B错;
,B错;
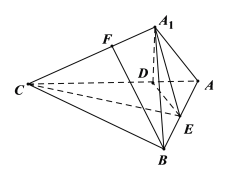
设![]() 是
是![]() 中点,连接
中点,连接![]() ,则
,则![]() ,所以
,所以![]() ,从而
,从而![]() ,
,![]() 是
是![]() 中点,所以
中点,所以![]() ,若
,若![]() ,即
,即![]() ,所以
,所以![]() ,所以
,所以![]() ,且由
,且由![]() 得
得![]() ,所以
,所以![]() ,
,
![]() 边长为4,则
边长为4,则![]() ,
,![]() ,
,![]() ,
,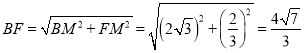 为定值,C正确;
为定值,C正确;
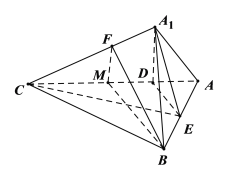
折叠过程中,![]() 不变,
不变,![]() 不动,当
不动,当![]() 到平面
到平面![]() 的距离最大时,四面体
的距离最大时,四面体![]() 的体积最大,由选项
的体积最大,由选项![]() 的判断知当
的判断知当![]() 平面
平面![]() 时,
时,![]() 到平面
到平面![]() 的距离最大且为
的距离最大且为![]() ,又
,又![]() ,所以此最大值为
,所以此最大值为![]() ,D正确.
,D正确.
故选:ACD.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目